南　泰裕

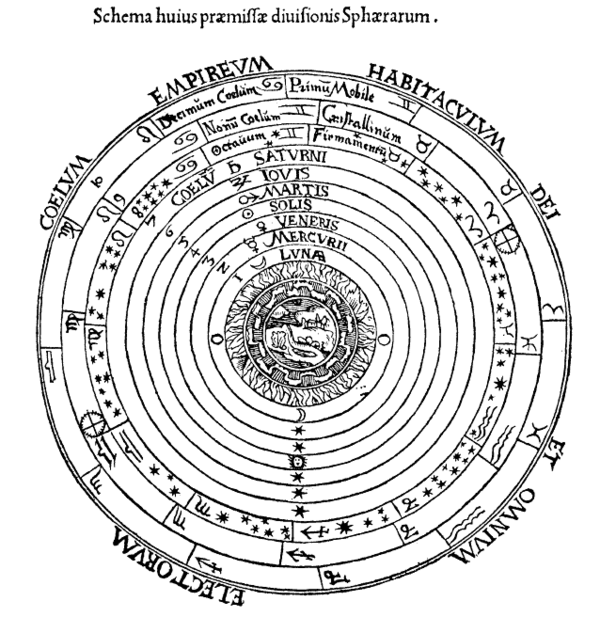
1　抽象と具体の邂逅 

イタリアでの後期ルネサンス建築が翳りを帯び始め、バロックの熱波がヨーロッパ全土を覆い熟成しつつあった、1684年1月のある日。 

ロンドンのコーヒーハウスに、一つの話題を熱心に語り合う、3人の男の姿があった。ハレー彗星で有名な天文学者のエドマンド・ハリー、物理学者で天文学者でもあったロバート・フック、そして建築家のクリストファー・レンである。イギリス王立協会で開かれた会合のあとで、3人はこのとき、コーヒーの香りを分かち合いながら、のちに科学の歴史を書き換える、重要な問題を議論していた。 
惑星の軌道について、である。 

これは、広く「ケプラーの法則」として知られるもので、「引力が距離の2乗に反比例する」という万有引力の法則に従えば、惑星の軌道は楕円になるだろう、という予測だった。けれどもこのコーヒーハウス談義の際には、この難問についての満足な解答を、誰も出すことができなかった。そこで後日、ハレーは一心、アイザック・ニュートンを尋ねて教えを請う。ニュートンは即座に、この問題に対する卓越した知見を伝授し、ハレーはそこから革新的な教示を得て、ハレー彗星の軌道を見事に予測することになる。 

ここで興味深いのは、この1684年という年が、ライプニッツによって、世界で初めて微積分の論文が発表された年だ、ということである。と同時に、その微積分の萌芽をなす楕円についての数学的研究が、惑星軌道の予測をめぐる天文学および物理学と、はっきり接続した年でもあった。そしてその、自然科学の歴史的転換点の渦中に、建築家のクリストファー・レンが立ち会って（というよりもむしろそこに深々と参与して）いたのである。 

つまり、極めて抽象度の高い「微積分」という手続きと思考が、具体の物理現象に射影され、それがぴったりと折り重なった年だった。 

こうした、微積分をめぐるメルクマールとなる転換点に、建築家のレンが同時代的に関わっていたことは、建築の歴史を振り返る上で極めて重要な意味を持っている。言うまでもなく、建築はその始原以来、数学と無縁ではなく、より限定していえば、幾何学への眼差しなしには成立しなかった。しかし数学が高度化していく中で、それらは具体と実感の世界から遊離し、直感的な把握を拒む抽象的な論理体系へと変容し始めた。それを鮮やかに転倒させたのがデカルトであり、解析幾何学、すなわち代数と幾何を座標によって切り結ぶ方途を発見することで、論理の抽象と直感の具体をまっすぐに架橋したのである。 

しかし、ここで問うべきなのは、この点ではない。肝要なのは、微分積分学の誕生と経緯を、歴史的なパースペクティブでなぞって見たときに、それが建築へとどのように漸近し、何をもたらしたか、を問うことである。さらに言えば、微分積分という概念が、建築を通過することで見えてくるものは何か、を問うことである。 



２　古代ギリシア・ローマにおける従円天体モデル

微積分の発見は、17世紀後半における、ニュートン（1642-1727）とライプニッツ（1646-1716）による正式な論文発表を待ってその嚆矢とする。だが、その由来を遡れば、近代科学の父と呼ばれる、ガリレオ・ガリレイ（1564-1642）に辿り着く。ガリレオは物体の落下や大砲による砲弾の軌跡を研究し、それが放物線となることを明らかにした。つまり、物理的な物体の運動が、正確な幾何学的図形として描き出せることを発見したのである。 

しかし、ガリレオの後を受けて、微積分の誕生に最も大きな役割を果たした先駆者は、デカルト（1596-1650）だった。デカルトは古代ギリシアの幾何学から着想を得て、それを近世ヨーロッパに呼び戻すと同時に更新し、その後の数学的思考を根底から書き換える、優れた手法を発見する。座標という概念の導入である。 

古代ギリシアおいて、幾何学は最も重要な学問領野であった。例えばプラトンが創設したアカデメイアという学園の門には、「幾何学を知らぬ者、くぐるべからず」という標語が書かれていた、と言われている。それほどに、古代において幾何学は、学問全体の基盤をなす必要不可欠な分野とみなされていた。だからデカルトは、古代ギリシア幾何学に触発され、自らの哲学と思想の核心を展開した『方法序説』（1637年）において、「屈折光学」「気象学」「幾何学」という3分野を特権的に取り上げて思考を突き詰めた。ここで彼は、様々な曲線を考えていく中で、曲線を記述する指標として「法線」という概念に辿り着く。これはある曲線の一点における、接線に直交する直線のことであり、微分の要である接線と、ほぼ一対になっている。その後、デカルトが考案したこの接線に大きな影響を受け、それを発展させることで、ライプニッツとニュートンが微分・積分という体系を精緻に編みあげることになったのである。 

このように、微積分の展開を歴史的に遡れば、古代ギリシア数学（幾何学）と近世ヨーロッパの哲学・数学が、時を飛び越えて共鳴し、呼応している繋がりが見えてくる。 

そこで、ここではまず古代ギリシアにおける微積分の来歴と建築を併置させ、この両者を共時的に眺めわたしながら、近世ヨーロッパ時代へと繋げてゆくことにする。 

古代に遡行し通史的に見渡せば、微分・積分は、まず理念的図形としての円を引き寄せ、そこに天文学への眼差しを重ねることで展開してきた。その原型は、ピタゴラス（B.C.580頃-B.C.500頃）にまで遡る。ピタゴラスは宇宙において、地球を含む様々な惑星が、完全な円上を周回しているとし、ここに同心円状の幾何学的な宇宙モデルを生み出した。 

ピタゴラスのわずかに後で、天文学とは全く別の視座から微積分に肉薄し、その本質に近接していたのが、エレア派のゼノン（B.C.490頃-B.C.430頃）である。ゼノンは「アキレスと亀」や「飛んでいる矢」と言ったパラドクスを編み出したことで知られている。これらのパラドクスはいずれも、物体運動に即して「時間・空間」を無限分割していった先に何が現れるか、と言う問題系に集約される。つまり、アナクシマンドロス（B.C.610頃-B.C.546）がアルケーとしての「無限なるもの」（ア・ペイロン）を措定したのとは別の角度によって、現実の運動現象の中から「無限」と言う観念／アポリアを切り出したのである。時間と空間を限りなく最小分割し続けようとするゼノンの見立ては、連続量の限りない微小化によって現象の傾向（接線）を記述しようとする、微分の手続きそのものである。ここにすでに、微分の概念が明瞭に胚胎していた、と言って良い。 

その後、アリストテレス（B.C.384-B.C.322）は紀元前4世紀に、中心に不動の地球があり、その周りを月や太陽、星が円運動をしているという、完全な定常状態としての宇宙モデルを提示した。いわゆる天動説の先駆けであり、その後200年近くもの間、人類の知見を支配したモデルだった。 

こうした天体観測と交錯する形で、測量の技術としての積分が、先に追究された。古くは約4000年前のエジプト時代に、すでに図形の体積や面積を求める積分の萌芽が見られる。が、幾何学的図形を対象に、積分的技法を初めて本格的に定立させたのは、古代ギリシアの数学者であるアルキメデス（B.C.287?-B.C.212）である。アルキメデスは「取りつくし法」という多角形分割の手法により円周を計算し、紀元前の時代に円周率3.14という極めて精度の高い数値を確定することに成功した。これは間接的に、図形の正確な面積計算に肉薄しようとする、積分の概念にいち早く触れていた技法だった。 
こうした先駆を経て、ローマの学者であるプトレマイオス（83頃-168頃）が、古代ギリシアの天文学を集大成させ、天動説としての従円モデルによる宇宙像を構想する(Fig.1)。ここでは火星や金星等を含めた各惑星間の距離と配置を定義し、観測現象と完全な同心円モデルを調和させた、精緻な天体モデルを編み上げた。

3　古代ギリシア・ローマ建築における円と楕円

このように、微積分の揺籃はまず、はるか遠く約2500年前から、幾何学的理念としての「円」と、物理現象としての「天体」を切り結ぶ一方で、「無限」と言う観念を思惟するところから始まった。 

ではその頃、建築はどうであっただろうか。言うまでもなく、古代ギリシアにおける知の展開と建築の揺籃は、その地歩において軌を一にしている。が、この時代に「微積分」と「建築」との交錯点を見いだすことは、まだ尚早だった。パルテノン神殿（B.C.447-B.C432）が姿を現した紀元前5世紀と言えば、ちょうどソクラテス(B.C.470-B.C.399)がアテネで活動し、ストア派のパイオニアをなすゼノンが、運動をめぐる不可思議なパラドックスを生み出していた頃である。この時期、幾何学的理念としての「円」が、痕跡線として明示的に建築へと転写された事例としては、例えばミレトス（紀元前5世紀頃）やプリエネ（紀元前350年頃）の野外円形劇場、あるいはエピダウロスの円形劇場（紀元前4世紀後半）といったものが想起される(fig.2)。が、そこに「世界を映し出す幾何学的図形としての円」という理念的な象徴性はない。

微積分と建築は、この頃、まだうまく交通し得ていなかったのである。 

局所的には、古代ギリシア建築におけるオーダーの断面が「円」として措定されるとは言える。だがそれらは、フルーティングやエンタシスといった人為的なオペレーションと多数性により、幾何学的な円というよりも、座標の交点をなすドットの様態として存立しており、理念としての「円」を表象してはいない。古代ギリシア建築の根幹は、威風堂々のオーダーが立ち上がり、均質に果てなく連続する柱と壁と直交座標による構築性にあり、あくまで矩形（および直方体）としての、人為的な理念的表象として存立していた。 

理念としての「幾何学の起源」（フッサール）を遡行することは、それ自体、魅力的な問いである。また、かつて伊東忠太が考察していたように、建築部位の装飾の次元までを含めれば、ギリシア建築においては正円や直線ばかりでなく、複雑な曲線の多様な展開が見て取れるため、そこから様々に複雑な次元の「直線と曲線の考古学」を見いだすことも可能である注1)。が、こと「微積分」と「建築」の揺籃の時代として古代ギリシアをみる限り、これら二つがはっきりと切り結ぶ契機を抽出することは、できないかに見える。ただし人類史的なパースペクティブによって遠望するならば、始原としての建築は直線よりも曲線、長方形よりも円として立ち現れたとするのが通説である注2)。原始的な伝統的住居は、概ね円形や馬蹄形、長円形平面から始まっており、長方形平面の出現までには遠大な時間を要している。簡単に言えば、文明の始まりにおいて、不定形の曲線をファジーに生み出す方が、矩形の直角を導き出すよりも、ずっと簡易だったからである。
 
翻って、例えば物理学者の湯川秀樹は、相対性理論における「曲がる空間論」に関連して、次のように述べていた。「自然は曲線を創り、人間は直線を創る・・・しかしさらに奥深く進めば再び直線的でない自然の真髄に触れるのではなかろうか。ここに一つの問題、特に理論物理学の今後の問題があるのではなかろうか」注3)。ここには、曲線としての自然が人為的な直線に置き換えられた先で、さらに高度な曲線を正確に記述しようとする、微積分の概念につながる視点がある。また、ル・コルビュジは『ユルバニスム』（1924）において、不定形に曲がった道を批判し、直線の街路こそが人間的だと主張している注4)。所与の自然としての曲線（円）を、人為として直線（矩形）へと仕立て直すことこそが、知の立て上げに他ならない、という訳である。 

そうした中で、人類の知の一端を拓いたギリシア人たちは、自然の模倣としての円から離脱する、理念構築の契機として、反自然的な直線と矩形の美学を立ち上げた。 

だとすると、古代中国における「天円地方」よろしく、完全な宇宙的調和のシンボルとしての「天にかかる円」と、人間による合理的理念の表象としての「地に建つ方形」が、天と地を分かつ分水領として鋭く対峙する、という図式自体が、ギリシアにおいても受容されていたと考えて良い。それが、古今東西を問わず、広く集合知として分有されてきたのではないか。そこで、建築の起源をなすと言われる「太陽信仰」と「地母信仰」を対位法的に翻訳するかのように、次のような対比的図式を素描することができる。 

・円−天体／従円モデル−自然／曲線−中心／周縁 

・方形−建築／理念的モデル−人為／直線−均質／反復 

こうした対比と峻別を、しかし、劇的な空間によって止揚したのが、他ならぬパンテオン（118-128）の出現だった。 

直径43.2メートルの球体を内包したこの驚異の建築は、完全な調和に貫かれたミクロコスモスとしてのドーム空間を実現させるため、外部からはほとんどなりふり構わぬ構造形式により無骨に円形平面の壁体を外部から支持している。また、矩形による前面の玄関柱廊は、正確無比の完璧な円堂にダイレクトに突き刺され、矩形と円形の対比を鋭く際立たせている。ドーム内部では、直径9mからなる天上の丸いオクルスから光が降り注ぎ、頂部へと向かって収斂してゆく格天井の格子を舐めるように照らし、それが移ろいながらくっきりと時を刻む(Fig.3)。

これ自体、まさにピタゴラス以来の、従円による天体モデルの奇跡的な縮減であり、物象化であった。中心に立つ人間を世界に定位し、天空をその手元に引き寄せる、「人間／惑星／恒星／天体」の同心円による、宇宙モデルの出現であった。 

そしてこの、ミクロコスモスとしての建築の完成が、プトレマイオスによる天体・宇宙モデルの創案と、完全な同時代をなしていたことは、単なる偶然ではなかったに違いない。時代的にも場所的にも、プトレマイオスの宇宙モデルとパンテオンは、共鳴していた。
 
ここにおいて、先の二つの図式が重合し、その後はるか先における、近世ヨーロッパでの「微積分」と「建築」の高度な展開を、予見的に先取りしていたのである。
 
宇宙を映し出すミクロコスモスとしてのドーム建築と、地球を中心とする宇宙モデルによる天文学、そして幾何学の最上位形態である円。これら三様は、ここに至って完全な調和を持って接合し、三位一体の見事なトライアングルを形成したかに見える。しかしそのモデルに亀裂を入れ、後の微積分をめぐるドラマツルギーを予示した建築を、ここで忘れるわけにはいかない。
 
コロッセウム（72-80頃）である。古典主義建築の教科書をなす巨大なこの野外劇場は、長軸188m,短軸156mからなる楕円形をなしており、平面的にも立断面的にも動きを孕んだ動的なプロポーションとなっている(Fig.4)。コロッセウムは、闘技場という、その血なまぐさい用途から、歪んだ円としての楕円により造られた。だとしたら、静謐と理知の象徴としてのパンテオン（円／球）と、喧騒と動態を射影したコロッセウム（楕円／逆円錐）は、同時代において「円／楕円」という天体モデルを両義的に写し取り、転倒した鏡像関係をなしていた。そのため、この両者それぞれが、「微積分」の概念に接続してもいた、とも言えるだろう。

4　近世ヨーロッパにおける楕円の天体モデルと、微積分概念

古代ギリシアにおける数学（幾何学）と建築の交差の機運は、ローマ帝国衰退後、ヨーロッパにおける「暗黒の中世時代」による停滞のため、長らく雌伏の期間を持たねばならなかった。スコラ哲学の閉塞から離脱し、ほぼ1500年もの間、揺らぐことのなかった、プトレマイオスによる地球中心の宇宙モデルをようやく突き崩したのは、コペルニクス（1473-1543）である。コペルニクスは、はるか昔に置き去られたプトレマイオスのデータを詳細に読み解くことにより、太陽を中心に惑星がその周りを回転する、太陽系による「従円・周転円モデル」を組み上げた。そしてコペルニクスが亡くなった1543年に、彼による『天体の回転について』が刊行され、地動説が初めて世に問われることとなる(Fig.5)。これにガリレオ・ガリレイが強く反応して、コペルニクスのモデルを支持し、地動説の画期をなしたことは、よく知られる通りである。 

ここでようやく、微積分誕生の通史を一旦棚上げし、「微積分とは何か」と言う基礎（論）的な問いを、建築に沿って召喚する地平が、見えてきたかに思える。 

一般に、微分は「幾何学的な曲線の接線／傾向」を示し、積分は「様々な図形の面積／体積」を示す、と言うのがごく普通の数学的な定義である。事実、後述するように、微積分の発展に驚異的な功績を残したデカルトやライプニッツも、繰り返し、はっきりとそのように述べている。曰く、曲線の性質を知ることが微分の目的であり、図形の面積を知ることが積分の目的である、と。また、歴史的には積分の技法が先に進歩し、その後に微分が生まれ、それらの逆転した倒立関係をニュートンが明らかにした、というのが、紛れない定説となっている。 

しかし、微積分の通史や一般了解を再確認するたびに痛識するのは、そのような、微積分の定義と理解をめぐる、微妙な不全感である。 

よく知られているように、技法としての微積分の具体的効用は、様々形で応用されている。と言うよりも、高度なテクノロジーが複雑にかけ合わされた現代社会においては、微積分の技法を直接間接に、下敷きにしていないものはない、と言っても良いほどである。微積分の技法は、最小化や効率化、最適化、時間概念といったものとの親和性が極めて高いため、絶えずテクノロジーの進歩と並走し、寄り添う。曲率のオペレーションとしての高速道路の設計や、発電機の最大効率、流体的フォルムのカーデザイン、人工衛星の速度計算やCTスキャンの設計、さらには金融工学における確率論等、例を挙げれば枚挙にいとまがない。建築の免震技術においても不可欠な手法であることは、改めて指摘するまでもない。 

しかし、そのような現実の効用からいったん目を離し、これの概念の意味を問うてみると、途端に、思惟の所在なさに当惑してしまうように感じる。 

微積分という概念の発見と展開は、メタフィジカルな見立てにおいて、何を意味しているのだろうか。 

さらにその先で、微積分は建築に、どのような原理的な意味を持つのだろうか。 

暗黒の中世が明けてコペルニクスが発見的に展開した、地動説としての宇宙モデルは、しかし、まだ天体の運行を円によってトレースしていた。コペルニクスの知見を参照しつつ、これを楕円によって記述し直し、現実読解の解像度を一挙に上げたのが、天文学者のケプラー（1571-1630）である。ケプラーは師のティコ・ブラーエに観測技術を習い、火星の複雑な動きを調べることで、有名な3法則に辿り着く。すなわち、次の3つである（Fig.6）。 

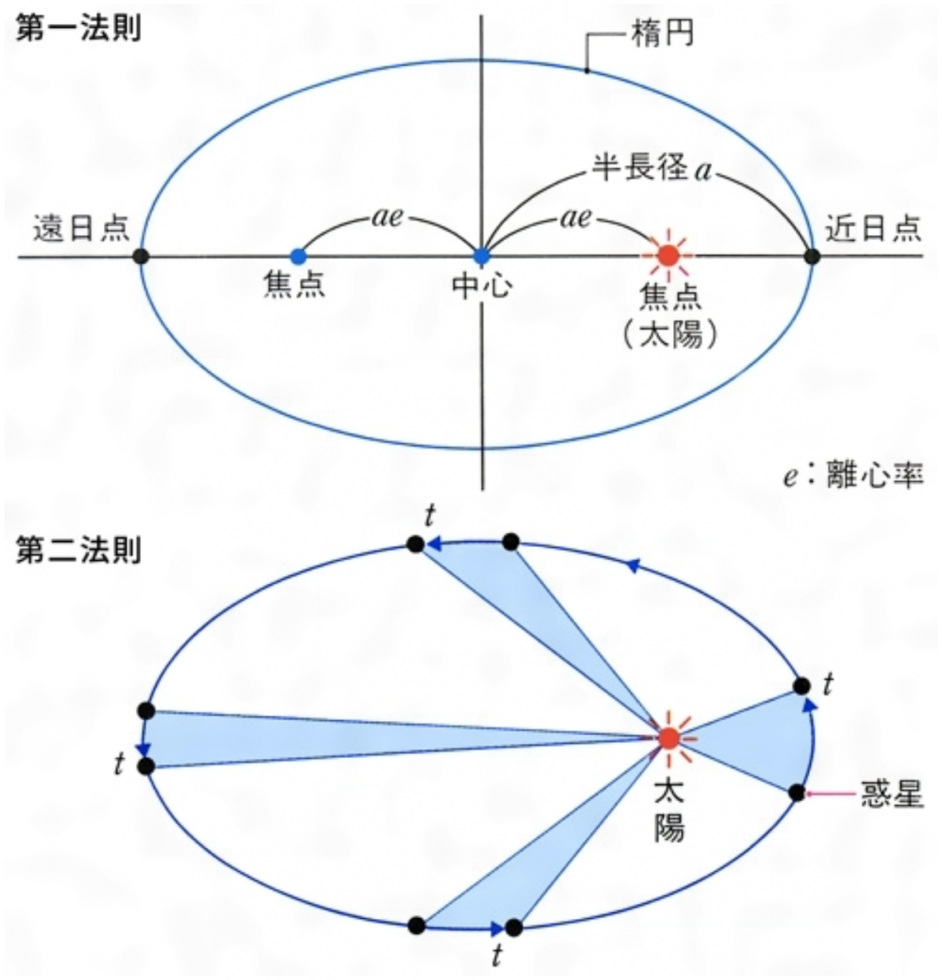
第1法則：軌道は円ではなく、太陽を焦点とする楕円であること 

第2法則：惑星運動の面積速度（太陽と惑星を結ぶ線分が一定時間に通過する面積）が一定であること 

第3法則：惑星の公転周期の2乗が楕円の半長軸（太陽と惑星の平均距離）の3乗に比例すること 

これは確かに、革命的な発見だった。というのも、人間の素朴な願望としての「調和的で均斉のとれた宇宙モデル＝円」を脱臼させて「楕円」を引き寄せ、現実の現象を正確に読み抜いたからである。さらに言えば、近代科学の要諦をなす「万有引力」と「微積分」を、ニュートンが奇跡的に同時構想する端緒を拓いたからである。ケプラーによる面積速度の一定則は、裏返せば「太陽による万有引力の釣り合い＋楕円の運動軌跡」、という力学的見立てに他ならなかった。 

こうして、コロッセウムが彫り込んだ楕円の陰影が、ミレニアムの時を飛び越え、近世へと写し込まれたのである。 

ここに至って「微積分」の来歴と天文学は、一度、袂を別つこととなる。ガリレオとデカルト、ニュートンとライプニッツたちが、天文学と幾何学を架橋しつつ、天を覆う宇宙から己の思惟の小宇宙へと、思考の舞台を移動させることになるからである。 

「近代科学の父」と呼ばれるガリレオは、運動と落下についての検証を繰り返す中で、物体を投げた時の軌跡を放物線によって記述し、自然現象／重力を幾何学的に定義できることを発見した。ガリレオによる運動法則や地動説は、同時代を生きていたデカルトに大きな影響を与える。そしてそれが、微積分誕生の重要な契機へと繋がっていく。 

デカルトは1637年に刊行された『幾何学』の中で、次のように述べている。 

「最も複雑な線もひとつの連続的な運動、または互いに連係していて最後の運動は先だつ諸運動によって完全に規制されるような多数の運動によって描かれる」注5) 

これは文字通り、様々な曲線を「動きの軌跡」として捉えた上で、その傾向／接線を導き出そうとする、微分の定義そのものである。古代ギリシアにおける幾何学の作図問題に触発されて、数学を発展させたデカルトは、この本において、いかに曲線を精密に定義し、描くか、ということを繰り返し述べている。また、その先で、古代の幾何学においては、双曲線や楕円といった「アポロニウス（B.C.262頃-B.C.190頃）による円錐曲線」を理解することまでが限界であったとして、複雑な曲線を正確に作図する方法を様々に試みている。 

デカルトはそうした試行の先で、様々な曲線の、任意の点における法線を作図する方法を発見した。デカルトにとって、曲線を知ることこそが、世界の成り立ちの謎に肉薄する、核心的な理路だった。デカルトの考察では、まだ微分における接線の概念には至らず、接線に直交する法線によって曲線を記述していたため、その対象となる曲線は限定的ではあった。だが一方でデカルトは、物体の円運動が、接線方向へのベクトルを孕んでいることを見抜いていた（Fig.7）。彼は円運動から放たれた物体の動きについて、『哲学原理』の中で、次のように言っている。

「運動するすべてのものが、運動の間に記され得る個々の瞬間において、直線的に或る方向に向かって運動をするべく定められており、決して曲線的にではないということである」注6) 

曲線（円）の接線を示唆するデカルトのこの認識は、物体の放物運動を「重力と進行方向」の二つに分割して定義しようとしたガリレオの運動則と、正確に呼応している。ここでは曲線の作図としての幾何学に、物理現象としての運動法則が、見事に融合させられていることが見て取れる。 

こうして、ガリレオによる自然観測という方法が、デカルトにおいて純粋幾何学の追究へと翻訳され、微積分を通して事象と概念、事実と理念がぴったりと重ね合わされてゆくことになる。 



5　バロック前期における楕円と、ライプニッツによる微積分 

天文学と幾何学の、予定調和的な重ね合わせによる「円」が地滑りを起こし、動きを孕んだ「楕円」へと変容し始めたヨーロッパは、まさにルネサンスからバロックへと移り変わる時期だった。楕円をめぐる、建築・都市におけるその先駆的な代表例は、ミケランジェロ（1475-1564）によるカンピドリオ広場（1536-47、ローマ、建築は別）だろう(Fig.8)。 

バロック的広場の先駆けをなすこの場所は、逆台形という敷地条件を読み込んで、バランスの取れた巨大な楕円が描かれており、その中心にマルクス・アウレリウスの騎馬像が立つ。ここでは丘から都市へと伸びる中心軸による厳格なシンメトリー配置を通して、ヴィスタを考慮した遠近法の効果を強調している。と同時に、次第に広がるアプローチの大階段と楕円の広場が、人を誘い込む動きと流れを生み出している。それにより、三方を取り囲む古典的なファサードを集約する求心的な視座を与えるとともに、それを長軸方向の直線へと変換させる、両義的な効果を与えている。さらに、その床面には12角からなる星型模様を組み入れ、ルネサンスの建築に多く見られる、スタティックな円のモチーフとは、劇的に異なった空間の気配を生み出している。 

この広場としての楕円に対して、建築として楕円を採り入れた最も早い事例の一つは、ヴィニョーラ（1507-1573）による、フラミニア通りのサン・タンドレア教会（1553、ローマ）である(Fig.9)。これは、シンプルな直方体の上部に楕円形のシリンダーが内接する形で載り、その内部が楕円型のドームとなっている、小さな建築である。そのため、矩形による平面と楕円型の天井が付き合わされ、その端部においては余剰としての部位が生まれて、不思議なヴォリューム感を形成している。建築において楕円の採用を実験的に試みた、試行錯誤の跡が読み取れるし、何より興味深いのは、吹き抜けとしての天井を楕円によって表現していることである。つまり、この天井自体が楕円としての天空／軌道を示唆する寓意として、読解できるからである。さらには、楕円に外接する下部の直方体自体が、楕円の微分である接線の包囲体として配されていることは、注目しておくべきだろう。

ヴィニョーラのこの建築は、単純であるがゆえに逆に、ある意味で極めて純度の高い形で、楕円という幾何学的概念が表象されている。だとすれば、先駆的なこの小作品が、バロックを彩るその後の巨匠建築家たちに大きな影響を与えたことは、想像に難くない。 

ただし、バロック建築と楕円との関係は単純ではなく、必ずしも両者の成立と発展が一致しているわけではない。伊藤哲夫は、ヨーロッパの楕円建築に関する考察の中で、楕円の空間は16世紀以降のマニエリスム時代に対応するとして、次のように述べている。 

「楕円の空間の成立は、本来的には北方の国々に起こった宗教改革に対する「反」宗教改革をモーメントに、キリスト協会の内部空間のあり方についての思考の中で、パンテオンを典型とするあの円形空間と教会本来の空間といってよいバシリカ（長堂式）の空間との間のコンプロミス、いわば妥協の空間として成立した」注7) 

つまり、伊藤によれば、建築における楕円は、円（集中形式）と矩形やラテン十字形（バシリカ形式）の融合として出現してきた、という訳である。さらに付言するならば、バロックにおける多くの楕円モチーフは、場のコンテクストを読み込むことにより、直線と曲線のストラグルを調停する結果として導出されている例も多々見られ、いわば都市と建築のせめぎ合いを架橋する図形モデルでもあった。 

ケプラーが楕円による3法則を初めて世に問うたのが1609年だったから、ヴィニョーラが楕円という幾何学的モチーフを、建築においてはっきりと具現化させたのは、それよりもはるかに早かった。それは、やがてバロックを覆う楕円の流行を、ほぼ1世紀近くも先取りしていたから、いわばプレ・バロックにおける、前倒しされたマニエリスムだった。 

このように、楕円／天体運行／万有引力／建築／微積分という概念の錯綜体は、この時期、ときに飛び火し、行きつ戻りつしながら、同時代を貫く複雑な知の磁場を形成し始めていたのである。 

微積分をめぐる、こうした揺籃と試行錯誤を経て、17世紀なかばに、科学の歴史を根底から書き換える、「驚異の諸年」が訪れる。1665年から1666年にかけての、ニュートンによる「万有引力の法則」「微積分法」「光の理論」の3つの大発見である。ガリレオやデカルトに影響を受けたニュートンは、ほんの数年で最先端の科学をマスターし、奇跡の発見にたどり着く。しかし慎重派のニュートンは、それらの成果を長い間公開せず、微積分を正式に公表したのは、40年も後の1704年に刊行された『求積論』においてだった。 

ニュートンはその前の1687年に、科学史上もっとも重要な書物と言われる『プリンキピア』を出版するが、ここでは恐らく意図的に、微積分の概念を使わなかったと言われている。 

そのため、ほぼ同時期の1675年に微積分のアイデアにたどりついたライプニッツが、ニュートンに先駆けて1684年に微積分を、世界で初めて世に問うこととなる。 

これが、冒頭における、1684年の、イギリス王立協会でのコーヒーハウス談義へと結びついていくのである。 

こうした錯綜した経緯のために、微積分の真の創始者をめぐり、ニュートンとライプニッツの間では、泥沼の争いが長い間に渡って続けられた。その争いに破れたライプニッツは、失意のうちに亡くなったとも言われている。が、現在ではこの二人ともに、微積分の発見者であると認められている。 

つまり、数学概念としての微積分は、ニュートンとライプニッツの偶発的で共時的な作業により、1665年に発見され、機が熟した1704年までには厳密に定義されて、人類の本格的な共有知となったのである。 

この時点で、微積分の基本概念は一挙に完成され、ライプニッツが考案した記号法を含めて、ほぼ今も変わりない形で様々に応用されている。 

それほどに、この二人が組み上げた精緻なモデルは、きわめて完成度が高かったのである。 

ただし、ニュートンとライプニッツの微積分に対するアプローチは異なっていた。ニュートンは運動によって、その速度（接線）や流量（面積）により物理学的なアプローチから微積分を定義した。対してライプニッツは、幾何学的にdy/dxという微小三角形や、

∫ydx
∫ydx

という短冊状の極小長方形を使って、微積分を説明している。これらがたどり着く結果は同じだが、そのアプローチの違いに、両者の解法の流儀が表現されている。いわば、ニュートンの方法が動態／物理学としての微積分であるのに対し、ライプニッツのそれは、静態／幾何学であったのである。 

こうした違いから分かるように、ニュートンが「驚異の諸年」に発見した万有引力と微積分は、いずれも現実の物理現象を抽象化することにより、極めて美しくシンプルな原理を導出したものだった。ここで興味深いのは、ニュートンは、自らが定義した「絶対空間・絶対時間」の概念を、いわば自己解体するような思考を展開していることである。すなわち、物理的な運動を定義する、絶対座標としての時空間（という前提）を、運動の軌跡としての微積分により、描き直す形となっている。というのも、微積分やリーマン、ロバチェフスキーらによる非ユークリッド幾何学といった数学的な道具立ては、やがて20世紀の科学を揺るがす相対性理論を準備し、相対空間・相対時間の概念と体系を導くことになるからである。ニュートンの絶対空間・絶対時間の概念は、彼自身により打ち立てられたと同時に、それ自身（微積分）によって内側から解体させられたとも言えるのである。 

事実、ライプニッツはニュートンによる絶対空間・絶対時間の概念を強く否定し、空間と時間は、「モノ・コトの秩序（配置）と関係」であると定義している。ライプニッツは空間と時間について、次のように述べている。 

「時間tempusとは同時存在しないものが存在することの秩序である。したがってそれは諸変化の一般的秩序であり、そこでは変化の種類は考慮されない」 

「空間spatiumとは共存する秩序、すなわち同時存在するものどうしが存在することの秩序である」注8) 

ライプニッツはこうした認識のもと、無矛盾の形で微小・極大概念としての微積分を創案している。重要なのは、こうした流れと展開から見えてくる、メタレベルの諸問題である。 

すなわち、微積分という概念は、リテラルには「曲線の接線・図形の面積を求めること」と定義されるが、これらの概念が照準しているのは、古来から大いなる謎として立ち上がり続ける「時間・空間」という形式のありかを問うことだった。 

微積分は、だから、それ自体が空間と時間の定義を裏側から支えている、と言って良い。ライプニッツが時空間形式を関係によって記述しようとするのは、まさに微積分によって、例えば図形のような抽象化された「存在しえない対象」を、幾何学的な明証性とは別の角度から輪郭化しようとする試みに他ならない。言い換えればそれは、「時間とは何か」「空間とは何か」という問いに対し、例えばそれを「ア・プリオリな超越論的形式」（カント）と言った述語的定義によって記述するのではない。そうではなく、時空間の概念そのものを図形へといったん映し取った上で、「曲線の傾向／無限小なものの無限集合」という＜関係と秩序の母胎＞へと、問いをずらしているのである。 

そしてここに、一見、特殊な数学的技法として映る微積分が、空間としての建築へと接続する契機が見出されるのだと思える。 

だからこそ、例えばジル・ドゥルーズはライプニッツのモナドとバロック建築のインフォーマリティを繋ぎ、「襞」の組成と関係を通して、空間を描き取ろうとしたのではないだろうか。すなわち、建築の成り立ちを「物的対象としてのボリューム／虚としての空間」という二分法で把捉するのではなしに、それを「さざ波の微小切片による、シンセサイズされた様態」として描きなおす、ということではないだろうか。 

概念としての微積分を考えるにあたって、我々はここで、フッサールによる『幾何学の起源』を想起し、それがなぜ、幾何学そのもののコンクリートな諸課題を（ある種徹底的かつ意図的に）取り扱わなかったのかを、今一度、問うてみるべきだろう。フッサールは幾何学の起源を問題化するに際して、例えばユークリッド幾何学における平行線公理の来歴といったような、幾何学そのものへの言及を、全くと言って良いほど行っていない。そこで語られている核心は、学問としての幾何学が、なぜ、現在のように構築されたか（そして、なぜその他のような形式ではなかったのか）という、知の制度の不可避的組み立ての歴史的規定性を巡る読解である。言い換えればフッサールはそこで、幾何学という（学問全体を象徴する）知の枠組みが、なぜこのように展開し、それが人類の知にとっていかなる意味を持っているのか、という、「学問の制度性」と呼ぶべきものを、根源的に問おうとしている。だから、幾何学自体を迂回しているかのように見えるフッサールの問いは、読む者にとって不可思議なものとして写り込むのである。だからこそ、ジャック・デリダはフッサールのこの小論を驚くべき解像度で読み込んで、幾何学は「根源的な純粋さのうちで捉え直されるとき、対象を構成する」と述べ、幾何学という学問が固有の輪郭で立ち現れることの意味を根本から問い直している注9)。 

これは、翻ってみれば数学（幾何学）とは一体、何を対象とし、何をなそうとしているのか、という問いに繋がっている。例えばラッセルは数学に対するそのような疑問に対し、次のように言っている。 

「数学は、われわれが語っていることが何（what）であるかということも、またそれが真であるかも知らないような学問だと言えるだろう」注10) 

数学に関するこの有名な言明は、多くの人に対し、確かに、腑に落ちる感覚をもたらしている。そのような言明を受け止めた上で、微積分と幾何学に建築的な審級を重ね合わせた時に見えてくるのは、次のようなことである、と考えられる。 

すなわち、微積分は、具体の物理現象と理念としての抽象をつなぐ両義性によって、幾何学に漸近している。微積分は、具体的現象の不可思議さに肉薄する、外化不能な論理の似姿である。言い換えればそれは、把捉不可能なモノ／コトへの漸近と接近の先で現れる、概念のゆらぎである。それは幾何学であると同時に、ない。言い換えればそれは、古来、自明されてきた学問の構築性を脱構築する手続きの一つである。世界の組成の全体を（そして建築にとっては＜ボリューム／空間＞の二分法的総体を）、認識不可能な無限小の切片によって一挙に読解する簡明な技法であり、極小が極大にダイレクトに接続する奇跡的な飛躍である。無限に小さいものが、世界の全体を無限大に正しく記述する。 

それを持って、われわれはここで、ミース・ファン・デル・ローエの‘God is in the details’（神は細部に宿る）という名言を想起しないわけにはいかない。ミースのこの言葉は、モノとしての建築の部位に照準されている。だが、微積分という概念を建築へと重ね合わせるとき、われわれは「モノ（実）と空間（虚）」という分別において複雑に定義される建築の、その両者を往還する何ものかへと限りなく近接しているのではないだろうか。言い換えれば、モノと空間との境界条件そのものを問う手続きこそが、建築と微積分との交錯点として、立ち上がってくるのではないだろうか。 

実際、われわれはバロックの都市と建築に、微積分のモデル図形の一つである楕円のモチーフを数多く見いだすことができる。が、それらはときにモノとしての楕円であり、空間としてのそれであり、囲い込む広場の形であり、あるいはイコンとしての図像的表現であり、様々な次元と位相を横断している。単純に、「バロックは楕円を主たるモチーフとしている」と言う言明では収まらない概念の拡張が示唆されている。そこでは、楕円という概念を通過させることで、それらの物的な存在様態が背後に退いているかのようである。実と虚の境界そのものを溶解させながら横断し、それらそれぞれの特性を記述する、見えない物差しとして機能しているかのようである。例えばデカルトはそれを、無限に広がる座標系としての「延長」の概念で捉えた。が、微積分はその「延長」の時空次元をさらに高度化し、動き自体を描き取ろうとする。それは、事物の成り立ちを、静態／動態を重合させた多様体として描きとろうとする、アモルファスな記譜法だった。 

微積分はその意味で、モノの組成と挙動による物理的現象を正確に記述する、優れて数学的な道具であると同時に、虚と実、という二項対立的な認識の枠組みから離れた、＜持続としての次元＞を拓く、「概念のねじれと外部」を指し示している、と言えるのではないか。 



6　バロック後期の都市・建築における楕円空間

数学・物理学における微積分の発見と展開は、バロック時代の建築が多彩に繰り広げた「楕円」の競演と、見事に時代が折り重なっている。その代表的建築の一つが、ボルロミーニによるサン・カルロ・アッレ・クワトロ・フォンターネ（1638-46、ローマ）である(Fig.10)。

バロック建築の最高傑作の一つとされるこの小さな教会は、「複雑性をもつ全体」（ギーディオン）と形容されるボルロミーニの建築的特性を、最も鮮やかに表出している。クリスチャン・ノルベルグ＝シュルツによれば、この建築ほど、平面分析が繰り返し行われた建築はない、と言う注11)。それは極めて厳しい角地の敷地条件の中で、波打つファサードから複雑な天井構成、細部のデザインや視線の制御に至るまで、異様な密度のデザインを実現させている。それにより、凝縮されたバロックの真髄を一挙に花開かせ、激情に充ちた造形を通して、細部まで徹底的に作り込まれた、ダイナミックな空間を実現させている。その真骨頂をなすのは、中央の楕円形ホールである。もとは矩形だった平面を不整形な十字形へと変形させ、それが上部に行くに連れて楕円形へと変換させられており、そこに多様な格子図形がはめ込まれて、極めて特異で複雑な平断面が創り出されている。ここで採用されている楕円は、正確には2つの正円を隣接させ、それを曲線によりつなぐことで生み出されている。つまり、円と矩形の中間的な形態が導出されており、敷地と機能の厳しいせめぎあいの中で、矩形を変形したような、スーパー楕円に近い長円形が導出されている。 

この建築ではさらに、歪んだファサードを強引にまとめるかのように、楕円形の大きなメダルが外観頂部にシンボリックに取り付けられており、楕円への確信的な偏愛を読み取ることができる。極めて小さな敷地の中に、自身の（そして時代の）世界観と建築観を、驚くほどの高い密度で表現しており、不定形の美学に沿って、部分と全体の弁証法が、楕円を通して花開いた建築だった。 

バロック時代における、もう一つの楕円の代表として挙げるべき建築は、ボルロミーニのライバルであったベルニーニによる、サン・タンドレア・アル・クィリナーレ教会（1658〜1670、ローマ）だろう(Fig.11)。前述の、ボルロミーニによるサン・カルロ教会からほんの数百メートルの位置に建つこの建築は、ベルニーニが代表作と自負した建築である。ここでは敷地の悪条件から、楕円を横使いとして、入口と主祭壇を短軸上に配しており、伸びやかに設えられた、楕円による円蓋が、優雅な気配を醸し出す。それにより、ボルロミーニのサン・カルロ教会とは対をなすような、楕円による空間的効果が、内外に渡り純度の高い形で表現されている。また、シンメトリーによる全体構成やクーポラ頂部に設えられた天窓等は、まさに歪んだパンテオンを思わせる。

ベルニーニにおけるこの建築も、使われている図形は厳密な楕円ではなく、擬楕円である。が、卵型の平面形態を基準に、内形を正確にオフセットする操作により外形が決定されているため、その曲線はより優美で整っており、端正な幾何学的プロポーションを強く感じさせる。 

ベルニーニはイエスズ会に対する信仰への深い共鳴から、この建築を無報酬で設計している。バロック建築の代表をなす傑作が、当代一流の建築家であったベルニーニであってすら、ボランティアによって生み出されていたことは、興味深いエピソードではある。 

このベルニーニによる小建築との、強い形態的アナロジーを持つ作品が、同じくベルニーニよって生み出された、サン・ピエトロ広場（1656〜67、ローマ）だろう(Fig.12)。

サン・ピエトロ広場は、大聖堂前の逆台形と楕円の組み合わせからなっており、全体としては前方後円墳のような輪郭をなしている。ただし、ここでの楕円は、施工上の技術的問題ゆえ、実際には2種類の円弧を部分的に重ね合わせて楕円となるよう設計されおり、厳密に言えば擬似楕円である。また、大聖堂前の逆台形は、ミケランジェロによるカンピドリオ広場がモデルとなっている。そこに、ベルニーニは幅240メートルからなる広大な楕円広場を付け加えた。これはベルニーニが、大きく腕を広げた人を模して、大聖堂と広場を関係つけようとしたもので、そこに天と地を繋ぐアントロポモルフィスムを読み込むことも可能だろう。が、ベルニーニによるこの楕円広場は、もともと、コロッセウムの楕円をモチーフとしていると言われており、そこにはカンピドリオとコロッセウムという、二つの楕円がオマージュとして映し込まれているのである。 

加えて、楕円を短軸方向に配置することで、中心軸に直交する視線の広がりを生み出しており、その構成はサン・タンドレア・アル・クィリナーレ教会との強い類似性を感じさせる。さらには、楕円の擬似的な焦点となる2つの場所を「円柱の中心」（centro del colonnato）として定位し、この地点から見れば、4列に連なる全ての柱が重なって、一本に見える操作を行なっている。 

これは、二重化された楕円の中心を示唆するとともに、「中心軸の延長と囲繞の求心性」「視線の拡張と収縮」の同時性を生み出しており、広場全体に、解放と閉鎖の両義的性格を巧みに付与しているのである。 

そうして、バロックにおける楕円というモチーフは、このサン・ピエトロ広場の実現において、一つの頂点に達することとなる。 

そして、建築家のベルニーニが、この広大な曲線からなる楕円広場の創出に腐心していたまさにそのときに、ニュートンとライプニッツは、曲線を分析することで微積分の概念を精密に彫琢し、完成させようとしていた。 

はからずも、建築と微積分の概念が、共時的に交通していたのである。 



7　ニコラウス・クザーヌスと、微積分モデルとしてのモナド

このように、天文学と神学、幾何学と運動という次元が重層的に交錯する中から、円が楕円へとシフトし、微積分が創出されたことが見えてくる。 

古来、円は様々に完成されたもの、完全なるものの象徴を示す理念的図形（あるいは図形的理念）だった。古代ギリシアにおいて、プラトンを筆頭になぜ幾何学が最も重要視されたかと言えば、それが概念としてのイデアを最も明示的に示しうるからであった。例えば、円や正三角形という、現実には存在しない幾何学的理念としての図形や、無限に伸びる直線を思念する、といったことである。 

中でも図形としての円は、天文学と神学、無限と完全なるものを過不足なく繋ぎ、表象する最上級の図形である。だからこそ、古来よりアリストテレスからコペルニクスに至るまで、人間の実存的な定位と完全無比な世界観を描く基準として、円／球体モデルが揺るぎない根拠となり続けた。 

ニュートンとライプニッツにより打ち立てられた微積分は、そうした完成モデルを一挙に瓦解させたが、実はそうした機縁は、中世ヨーロッパに密かに胚胎していた。ライプニッツが微積分を展開するにあたり、中世哲学者のニコラウス・クザーヌスから大きな影響を受けたことは良く知られている。が、そのクザーヌスの思想はネオ・プラトニズムの思想に近接しながら、その後のジョルダーノ・ブルーノに飛び火している。中世におけるクザーヌスやブルーノは、ネオ・プラトニズムから「無限」なる概念を受け取り、それを現実世界へと射影する思考を展開しようとした。結果、ブルーノは天文学的な見地から地動説に類似する説を唱え、異端視されて、最後は火刑に処せられてしまう。が、ここではそれを措いて、微積分の概念を手探りで予見していた、クザーヌスの思想を見ておきたい。 

クザーヌスは、ニュートンやライプニッツが微積分を構想する200年以上も前に、『学識ある無知』において、数学的なアレゴリーを通して次のように言っている。 

「最大者は何ものとも対立しえないものであって、最大者がそのままで最小者である。それゆえ、無限なる一は万物を含蓄し、万物を合一する一のことである」注12) 

クザーヌスのこの言葉は、むろん、中世における神学的な要請に沿って展開されたものだが、この言葉が、ほぼ正確に微積分の定義の原型をなしていることには、驚くより他ない。クザーヌスは、神秘思想を数学的な思考と組み合わせることで、世界認識のあり方を組み立てている。彼は幾何学に依拠する形で、円と球および三角形を、完全なる図形と定義し、そこから「無限に大きい円」や「無限に大きい三角形」を思念することで、無限の観念を導き出している。ここで示唆されている、「最大者」と「最少者」の一致という語り方や、アナクサゴラスに由来する「万物が万物のうちにある」という「一と無限の合一」の寓意的認識に、注目しておく必要がある。これは、微分（極小）によって曲線の全体を把捉し、その逆である積分（極大）によって部分から全体を計り知る、という数学的定義と、ほとんど正確に呼応しているからである。 

さらに言えば、ライプニッツによって構築された「モナド論」は、モナド（単子）という言葉の呼び出しを、ネオ・プラトニズム経由でブルーノに負っている。ライプニッツはそのモナド論の中で、次のように言っている。 

「モナドとは、複合体をつくっている、単一な実体のことである。単一とは、部分がないという意味である」 

「モナドは、自然における真のアトムである。一言でい言えば、森羅万象の要素である」注13) 

言うまでもなく、ライプニッツがこのように語るとき、ここでの「アトム」を、例えばデモクリトスらによるアトミズムの概念に、決して重ねてはならない。ライプニッツが語るモナドは、「単子」という言葉がもたらしてしまうイメージとは裏腹に、均質化した微小粒子の集合のようなものとして（つまり球体状の物的な微粒子として）思念してはならない。それは、そのように固定化されたスタティックなイメージからはみ出てゆく、把捉困難な「変化／持続／交通」の残余概念としてあり、それこそが微積分というものの、思考の感触に他ならないからである。 

だから、ライプニッツのモナド論は、微積分の代替理論として読解されるべきである。ここで彼が言うモナドは「窓がなく」「互いにすべて異なっており」「絶えず変化し」「一のうちにすべてを含んでいる」。それぞれのモナドは、それぞれに世界を表出する。最小の一の中に、最大の多数性が包含されている。すなわち、最小が最大であり、無限の観念がそこで倒立しあっている。こうしたライプニッツの思考が、先のクザーヌスの神秘思想と鏡像的に呼応しあっていることは、言うまでもない。 

だから微積分は、単に数学的な技法ということを超えた、世界を認識するための迂回的な手続きである。世界をいったんひずませ、そのたわみの強度から本質を読み抜こうとする、ラディカルな世界認識の技法である。そしてライプニッツはそれを、モナドというモデルによって、アレゴリカルに描出したのである。ライプニッツはモナド論の草稿を1714年に書き上げるが、その後に、建築家のフィッシャー・フォン・エルラッハ（1656-1723）によって設計された、宮廷図書館（1723、ウィーン）の建築に、彼は強い関心を持っていた(Fig.13)。ここには、微積分と楕円および建築をめぐる、興味深い共鳴が見て取れる。というのも、ベルニーニのもとで研鑽を積んだエルラッハによる、この宮廷図書館は、ウィーンにおけるバロック建築の代表作であり、楕円による中央ホールとその濃密な装飾こそがその空間の主題をなしているからである。モナドとバロック、楕円と襞は、ライプニッツにおいて数珠つながりの連接概念だった。だとすれば、ライプニッツはおそらく、同時代の建築（が示唆する幾何学と運動の軌跡）を、メタファーにおいて捉えていた。

だからこそドゥルーズはライプニッツのモナドロジーを、バロック建築を通して読解し、それを離散的な微粒子ではなく、境界条件が定かでない、フラクタルに伸縮する「襞」として描き出したのである。ドゥルーズが創案したバロック・ハウスという概念は、だから、単に物質と精神の二項対立を書き換えるにとどまらず、イメージし得ないもの、輪郭化し得ないものの流れと持続の総体を、イメージし得ないモナドのままに描写しようとする試みであった。ドゥルーズはその初期において、「差異と反復」の形而上学を手厚く展開し、イデア（理念）が微積分によって無限に差異化（differentiate）される、力能の可能性を語っている。そこでは、微積分は運動を記述するということを超えて、運動を立ち起こす強度的なるものとして捕らえられている。ドゥルーズは微分について、次のように言っている。 

「微分は、まさしく純粋な＜力＝累乗＞（ピュイサンス）なのであり、同様に、差異的＝微分的な関係＝比[dy/dx]は、ポテンシャリティという純粋なエレメントなのである」注14) 

微分とは現象のスタティックな記述というのではなしに、それ自体、世界へと介在／挿入される力動の痕跡、というわけである。 

これに続けて、その初期の段階においてすでに、ドゥルーズは襞の前身となる「折り畳むもの」という概念を微積分に重ね合わせている。ドゥルーズによるこうした思考の軌跡からは、ライプニッツによるモナド論が、「差異と反復」の形而上学を経由して、微積分／無限の概念と重ね合わされていることを、見て取ることができるだろう。 

すでに述べたように、ライプニッツは『人現知性新論』において、空間は関係と秩序であり、無限な全体である絶対空間ではない、と指摘した上で、「関係的観念の最も重要なものの一つは、同一性のあるいは差異性の観念です」と語っている注15)。ここでの「差異性」という言葉が照準を当てている重要なものの一つは、時間と持続であり、それを把持することの決定的な困難さである。 

これは遠く、ゼノンのパラドクスに接続するものであり、ベルグソンが繰り返し問題化していた、「空間化され得ない、純粋持続としての意識と時間」に漸近するものである。無限小と無限大の観念の先端で、確定し得ない「いま、ここ」の極点を、どのように措定するか。それが、微積分の問題系の核心であり、そのことが時間と持続の認識へと繋がっていた。がしかし、ここで最後に問いたいのは、そのことではない。微積分と建築の関係を問うにあたり、ここで見ておくべきなのは、幾何学に時間を重ね合わせたとき、静と動の弁証法において見出されるものの履歴と意味である。 

そしてその問いが、冒頭におけるクリストファー・レンたちの関心へと、繋がっていくことになるからである。



8　幾何学のヘレネ、サイクロイド曲線

微積分の発見と展開に沿って、近代科学の黎明期に、多くの数学者や哲学者を魅了して止まなかった図形がある。サイクロイド曲線である(Fig.14)。

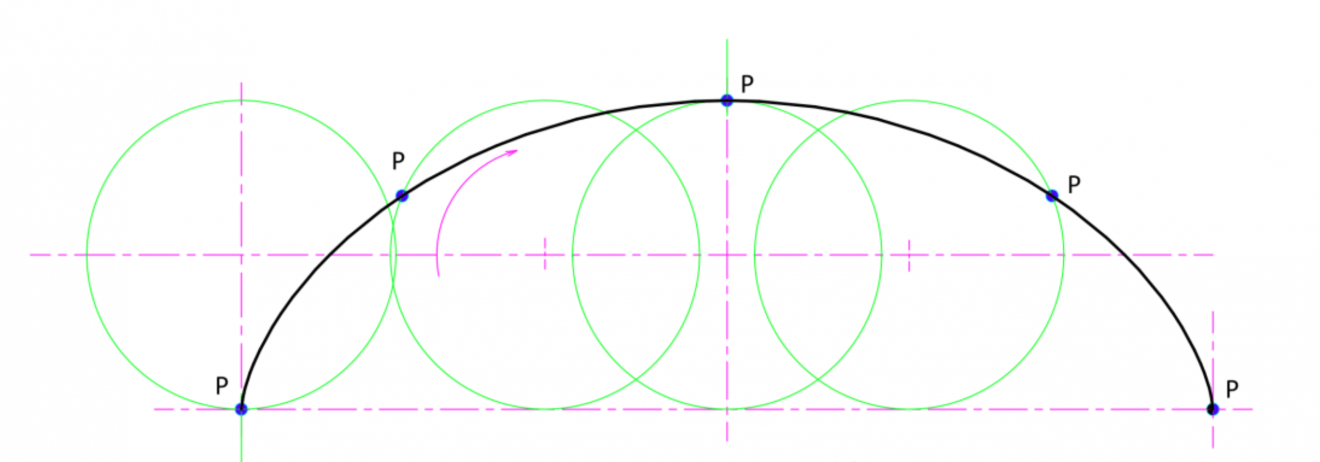
サイクロイドとは、直線上で円を転がしたときに、円周上の一点が描く軌跡の曲線である。この曲線にガリレオやデカルト、ライプニッツをはじめ、名だたる識者がこぞって関心を示し、それに関連する難問に繰り返し挑んだ。そのことから、サイクロイド曲線は、多くの人を魅了するギリシア神話の美女に例えられ、「幾何学のヘレネ」と呼ばれていた。単純な原理の曲線にもかかわらず、現実の現象をめぐる極めて豊穣で本質的な特性を持ち、それを長らくの間、誰もうまく解明できなかったからである。 

特異点を持つ波のように見えるこの曲線には、微積分の核心をなす性質と問題が多層的に内在している。その面積や弧長、接線や重心を求めることが、際立った難問となって、稀代の天才たちをことごとく駆り立てた。 

このサイクロイドに初めて着目したのは、ニコラウス・クザーヌスであると言われている。クザーヌスは古代ギリシアの三大作図問題である円積問題（円の方形化の問題）に取り組む中で、サイクロイドに着目した。が、これには様々な説があり、確定的なことは不明であるものの、無限と曲線、円と運動を考え続けたクザーヌスの著作から推し測れば、彼がこの曲線に関心を持った可能性は極めて高い。が、クザーヌスの思考におけるそれは、あくまでイメージを示唆するものにとどまり、数学と物理学を下絵とした、サイクロイドの厳密な理論展開は、ガリレオの出現を待たねばならなかった。 

数学的曲線としてのサイクロイドは、1599年にガリレオによって発見され、命名された。これは円から派生したという意味の言葉で、当時はルーレットとも呼ばれていた。 

おそらく直感的・無意識的には、サイクロイド曲線自体は現実に頻出する運動現象として、有史の極めて早い時期から認識されていた可能性はある。車輪である。直線上で円を移動するという現象は、まさに車輪の軌跡そのものだからである。世界最古の車輪はB.C.3000年頃のメソポタミア文明やインダス文明からも出土しており、人類は文明の起源においてすでに、サイクロイドを自身の発明と活動のうちに潜ませていたことになる。 

ガリレオは、振り子の揺れを時計に利用するアイデアを追究し、振り子の等時性にたどり着く。つまり、振り子の揺れ幅や重りの重さによらず、周期が近似的に一定になる、という法則である。これを厳密化したのが、ガリレオの弟子であったトリチェリや、時計作りに執念を燃やしたホイヘンスだった。 

トリチェリは1644年に『幾何学著作集』を出版し、その中でサイクロイド曲線の特性について言及している。また、ホイヘンスは、ガリレオの振り子理論を修正することで物理学的に厳密な振り子時計を考案し、1657年に、それを導くのがサイクロイド曲線であることを発見する。これは文字通り、サイクロイド振り子と呼ばれており、振り子時計が誕生したのは1673年だった。円弧としてのガリレオの振り子曲線を、サイクロイド曲線に変形することで、幾何学と物理現象を正確に結びつけたのである。 

こうして、振り子時計の発明という工学的要請と、サイクロイド曲線という数学的曲線が見事に重合する。一方でこの曲線の数学的特性をめぐる探究が、名だたる哲学者や数学者を引き寄せて、世紀をまたぐ歴史的難問として立ちはだかることになる。 

まず、サイクロイドと直線に囲まれた面積を求める求積問題に、ガリレオやデカルトをはじめとする科学者が次々と取り組んだ。が、ことごとく失敗していた。やがて1634年に、ロヴェルバルが面積を求めることに成功し、面積が円の3倍であることを証明する。ロヴェルバルのこの証明に、デカルト自身が悔しがったとも伝えられており、彼らがいかにサイクロイドの虜になっていたかが分かる。その後、サイクロイドに接線を引く方法も話題の数学問題となり、これも同様に、多くの識者たちが繰り返し失敗を積み重ねた。その試行錯誤の果て、サイクロイドの接線法をフェルマが発見する。 

が、サイクロイドをめぐる歴史の中で最も有名なのは、パスカルのエピソードだろう。1658年のある夜、36歳のパスカルは激しい歯痛に襲われ、その痛みを忘れるために、夜通しサイクロイドの諸問題に集中する。結果、サイクロイドをめぐる様々な難問を解決し、数学史上普及の名作となる論考を発表するに至る。サイクロイドの面積、重心の決定、その回転体の体積と表面積といった諸問題である。この論文は、当時世俗から離れていたパスカルがデットンヴィルという偽名で発表し、その優れた発見は世間に衝撃を与えた。そしてこの論文が、後年、ライプニッツに大きな影響を与え、微積分の発見へと繋がっていくことになる。事実、ライプニッツにおける微積分関連の数学論には、サイクロイドに関する言及が繰り返し見られる。それは、微積分の謎を集約的に表出する特権的な図形として、当時の識者たちの心を鷲掴みにしていたのである。 

サイクロイド曲線の解明に革命的な貢献をしたパスカルに対して、当時、ホイヘンスやフェルマをはじめとする最先端の研究者たちが、自分のアイデアや研究成果を伝えていた。その中でも特に重要だったのが、冒頭に登場していた、建築家のクリストファー・レンである。レンは1658年に、サイクロイドの周長計算に成功し、それが円の直系の4倍であることを正式に証明する。これは「レンの定理」と言われる有名な法則で、当時の人々にとって大きな衝撃を与えた。これは、かのパスカルですら解決できなかったことで、ホイヘンスは「これは素晴らしい発見だ」と、わざわざ当時の手紙の中で絶賛している。それほどに、曲線の周長計算は、微積分が発見される前には極度の難問で、多くの研究者たちを悩ませていたのである。 

レンはこの定理発見直後の1661年以降、ロンドンのセントポール大聖堂の再建計画委員となり、1675年の着工から35年の歳月を費やして、この大聖堂を完成させる(Fig.15)。そのインテリアにおいて、バロック様式の豪華な気配を彷彿とさせる、このラテン十字による新古典主義の建築は、しかしバロック的な流動性や楕円のモチーフや不定形の痕跡はない。形態的には、正円の連続と反復によるドームやアーチが連接しており、平面的にみると、円と円弧が自己相同的に、全体構成の基本単位となっていることが明快に読み取れる。

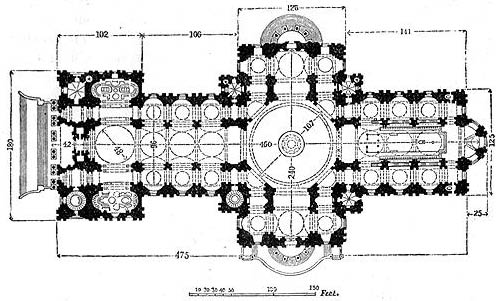
サイクロイドの特性を最もよく理解していたレンは、時代を席捲したバロックとマニエリスムによる錯綜の先で、円から楕円、楕円からサイクロイドという流れを還元し、円という形態に回帰しつつ、動きを孕んだ空間の創出にたどり着いたのではないか。 



9　空間記述としての微積分

サイクロイド曲線が、こうして当時の数学者にとどまらず、哲学者や建築家をも巻き込んで科学の焦点をなしたのは、それが幾何学的理念と現実の事象を、まるで奇跡の偶然のような形で、様々な次元において繋いでいるからである。そしてそれが、微積分の発見と展開の核心を、まっすぐ突き刺すことになったのである。 

一般にサイクロイドは、大きく2つの物理学的特性によって記述される。1つは最速下降線という特性であり、1969年にヨハン・ベルヌーイにより発見され、問題が提示されている。これは、ある曲線を滑り落ちる質点が、初速度ゼロで下降するとしたとき、最短時間で最下点に到達する曲線の形状は何か、という問題である。この解答が、サイクロイド曲線に他ならなかった。この問題にニュートンとライプニッツの2人も参入し、それぞれが自分が先に問題を解いた、と言い争っている。 

そしてもう1つは、ホイヘンスによって発見された等時曲線という特性である。これは、サイクロイド上にある質点は、その出発点の位置にかかわらず、降下時間は一定になるというものである。この特性の解明によって、ホイヘンスにより、前述したサイクロイド振り子が生み出され、正確な機械時計の発明に多大な貢献をすることになった。 

サイクロイド曲線のこれら2つの特性が示しているのは、次のようなことである。すなわち、直線上の円運動という、極めて単純な手続きから導き出されたサイクロイドが、実は運動の法則を潜在させた、いわば動きという事象を凍結させた特殊な曲線であったということである。つまりサイクロイドは、幾何学的図形を、スタティックな図像として定義するのではなく、運動と関係において（むしろそれによってのみ）描き出すことの表象をなしているのである。そして、サイクロイドのこうした特徴は、ライプニッツによる幾何学的図形と運動との関係化と、正確に呼応するものだった。 

ライプニッツは1695年に発表した数学論の中で、次のように言っている。 

「運動それ自体は、原因や力能（potentia）を考察しない限り、幾何学的に扱うことができる。というのも、線、いやすべての図形は、運動の跡だからである。私が考えるところ、運動の法則が定められたならば、時間、速さ、道筋を決定することは純粋に幾何学的問題である」注16) 

サイクロイドという幾何学的曲線は、まさに、ライプニッツのこのような認識によって立ち現れた、動と静を止揚する曲線（イデアと現象のシンセサイズ）である。実際、プラトンが語ったイデアは、そのモデルを幾何学の完全図形から得たと言われている。加えて、プラトンの問題系をスライドさせたアリストテレスが、最も重要な問題として取り組んだことの一つが、運動をいかに把捉するか、ということであったことを想起するまでもない。イデアを仮構する（可能態としての）幾何学と、物理的現象である（現実態としての）運動をいかに関係づけ同時記述するか、ということは、その始まりから、人類の知にとって抜き差しならない大問題として、常に立ち現れていたのである。そしてその一つの到達点として、サイクロイド曲線が存在したのである。それは完全なる静的な理念／天体宇宙モデルの象徴としての円に基づきながら、それを動かすことで、動態／運動としての幾何学を描き出し、微小と無限に繋がる微積分概念を生む契機をなしたのである。 

こうして見てきたように、幾何学的図形としての円・楕円・サイクロイドは、天文学と物理学を経由しながら、古代ギリシアと中世以降の知をつなぎ、理念と現実を、あたかも鋳型にはめるように正確に合致させた。円から楕円、サイクロイドという変遷を経る過程で、常に理念の物象化として存立していた建築に、その図像と形態が射影され、空間の手応えとドラマが、様々に確かめられた。 

初等幾何学の流れはその後、微積分の展開を契機として、楕円幾何学（球面状の特性を考える幾何学）や微分幾何学、およびその中心的主題をなす多様体問題へと発展していく。これは、様々な数学的空間における曲面や曲線の特性を明らかにしようとする分野で、「歪んだ空間」「曲がった空間」を対象とし、多様な局所座標系の同時存在を許容する図形や空間を対象としている。「各々が異なりながら同時に存在している」という様態は、あらゆる建築において、それぞれが固有の空間様態（個別の座標系）を有する、というイメージと折り重なってくる。これはやがて、重力による歪んだ時空間を取り扱う相対性理論へと繋がってゆく。建築学における「空間」というタームの定義域は、これら数学・物理学におけるそれと比較すれば、大いに厳密さにかけることは確かである。しかし、物象性を保証された建築空間の複雑な様態は、逆に、高度な空間記述の技法を要請する可能性を潜在させている、とも言える。だから仮に、微積分という概念を建築によって写し取るならば、それはいずれ、いまだ記述し得なかった建築空間を異なった角度から記述する可能性を示唆しており、それは今もなお探究する余地を多く残している、と言えるのではないか。 

数学的空間は、基本となる3次元空間から、三角不等式によって定義される距離空間、N次元空間、無限次元空間（ヒルベルト空間）へと発展し、さらにはそれらを包含するような、極度に抽象的な位相空間の高みへと進んだ。これらはもはや、単純で直感的な把捉を拒む抽象の極北に位置している。例えば、N次元空間を思念可能な形で瞬間的に思い描くことは、多くの人にとって極めて困難だろう。が、だからこそそれらの数学的な高次元概念は、建築空間の様態が生み出す、言語化できない「経験的空間」（ポアンカレ）の気配を、何かしら表記し得る可能性を孕んでいるのではないだろうか。例えばギーディオンらは近代建築の建築空間を、3次元に時間次元を付加した4次元として捉えていた。また、ロシア・構成主義の中心にいたマレーヴィッチやリシツキーたちも同様に、4次元空間を想定した考察をはっきりと残している。が、むしろそれをさらに高度化させ、仮に建築空間をN次元空間として措定し直すことで、新たに見えてくる建築の様相の断面があるのではないだろうか。 

いずれにせよ、これまで見てきたように、微積分の来歴をその前史と以後にまたがって見通して見ると、スタティックな世界モデルとしての円という幾何学的図形が、楕円からサイクロイドへと遷移し、さらには曲がった高次元空間そのものへと次元をあげながら、動き自体を内包していく軌跡が、見えてくる。そのため、曲線をめぐるそうした変遷は、動きを凍結させた物象としての建築に、つねにすでに、限りなく近接し続けてもいたのである。 


10　建築とサイクロイド 

実のところ、サイクロイドという曲線は、その始まりから、建築との関連性が示唆されていた。すでに述べた通り、この曲線は最速下降線と等時曲線という2つの特性持っているが、これはすなわち、時間と運動、および重力によって定義されているということである。これはまさに、物象としての、人間が知覚する環世界としての建築を、建築たらしめる要諦そのものである。そのため、例えばこの曲線を発見したガリレオ自身が、当初からアーチ橋の形態に最適ではないかと予測し、現実への組み込みを試みようとしていたが、当時はまだ、その原理をうまく解明できなかった。 

サイクロイドは、正円によるアーチと比較すると、横に広がった扁平アーチをなし、円弧の中心が多数ある多芯円に近似できる。そのため、擬似的にサイクロイド曲線とみなせるアーチ橋は、古くから存在した。例えばフィレンツエのサンタ・トリニタ橋は6芯円アーチである。すなわち、6つの円弧を接続させることで、擬似的に滑らかなアーチとして構成されている。一方で、サイクロイド曲線は限りなく5芯円アーチに近似できるため、サンタ・トリニタ橋のプロポーションは、サイクロイド曲線にほぼ重ね合わせることができる注17)。 

また、日本やアジアの伝統的な社寺仏閣の屋根には、「照り」や「むくり」の屋根が多く見られるが、これは多雨地帯における雨水処理や雨仕舞いと、密接に関係している。「流造り」という屋根形状の呼称は、文字通り水が流れるような形態から名付けられており、重力による水の流れと挙動を写し取った形態であることは明らかである。例えば法隆寺金堂の照り屋根は、ほぼサイクロイド曲線に近似できる(Fig.16)。サイクロイドが最速下降曲線であることを鑑みれば、この形態が最も早く屋根面の雨水を下部へと導くということが、当時の建設者たちに、直感的に見取られていることになる。実際にはこの金堂は、サイクロイドよりもさらに勾配の強い屋根となっている。が、これは、実際の水分の粘性や摩擦等の諸条件を考えれば、より現実の与件にアジャストされて最適化されている、と見做すことができるだろう。 

しかし何よりも、サイクロイド曲線を語るとき即座に想起される建築は、ルイス・カーンによるキンベル美術館（1972）ということになるだろう(Fig.17)。6本のヴォールトからなるこの美術館は、幾度となく試行錯誤が繰り返されたのち、最終的に正確なサイクロイド曲線による屋根形状として実現した。カーンはここにサイクロイドを採用することで、構造と設備、光と景観といった、建築の異なる次元を鮮やかにインテグレートさせている。サイクロイドにすることで、正円ヴォールトよりも高さを低く抑え、中央スリットからの間接光を天井面に柔らかく拡散させる空間効果を生み出している。ここでは、ポストテンションによるスパン30メートルのコンクリート屋根を、それぞれ4隅の柱で支持しており、垂直応力を一様化する構造的な要請から、この曲線が選択されたと言われている。がしかし、ここでのサイクロイドは、カーンが終生考え続けた、「光と力」の空間的弁証法として、選び抜かれたと言えるだろう。それは、曲面に沿って力を流すことの合理性を表象し、と同時に降り注ぐ自然光を天井面に沿って滑らかにゆっくりと流し落とすために、選ばれた形態だった。いわば、最速下降線というサイクロイドの物理的特性を逆立させて引き伸ばした、光の最遅下降曲面と言えた。それは遅延を表象し、できるだけ遅く長く、空間の気配を全体へと送り届けることで、光自体が無限に遅れて下降し降り注ぐ、重力と動きのメタファーとも言えたのである。サイクロイドが、この建築空間の粒だった独特の気配を生み出したのである。 

カーンのこの建築は、その意味で建築の微積分論に、繊細に接続した建築だった。そしてその先で、空間とは何かという、はるか遼遠から続く哲学的問いを、繰り返し喚起させる建築でもあった。 

微積分と建築の漸近をめぐる試論は、このカーンのキンベル美術館を持っていったん終わりとする。が、こうした来歴において繰り返し絶えず浮かび上がっていたのは、「建築における空間をどのように措定するか」、という避けることのできない重要な問題構制であった。つまり、微積分を建築に即して思惟しようとすれば、いずれ空間論にたどり着くよりない、ということだったのである。けれども空間論一般という主題自体を取り扱うことは、それ自体あまりに巨大で困難であり、とても筆者の手に追えるものではない。がしかし、それを建築へと写し取ったときに、例えば哲学的思惟における空間定義（デカルト、カント、ベルグソン、etc.）や、自然科学におけるそれ（ニュートン、ライプニッツ、ガウス、リーマン、etc.）と、どの地平において交錯し、何を新たに読み出せるのか、ということは、今もって考えておくべき課題だろう。新時代の、メタフィジカルな建築空間論が新たに望まれるべきであり、本稿は、それ向けてのささやかな試論である。 

－解説－

南泰裕（みなみ・やすひろ）／建築家、国士舘大学教授 

1967年、兵庫県生まれ。1991年、京都大学工学部建築学科卒業。1993年、東京大学大学院修士課程修了。1997年、同大学院博士課程満期退学。同年、一級建築士事務所アトリエ・アンプレックス設立。2007年、国士舘大学理工学部准教授。2012年、同大学教授。2015年、ミマール・シナン芸術大学客員教授（イスタンブール）。作品に「PARK HOUSE」「spin-off」「アトリエ・カンテレ」など。著書に『住居はいかに可能か』（東京大学出版会）、『トラヴァース』（鹿島出版会）、『建築の還元』（青土社）、『建築のデザイン・コンセプト』（彰国社）など。 

参考文献 
1) 高瀬正仁：微分積分学の誕生、SBクリエイティブ、2015 
2) 松下𣳾雄：曲線の秘密、講談社、2016 
3) 寺阪英孝：非ユークリッド幾何の世界、講談社、2014 
4) 河内康伸：サイクロイドとカテナリ、大学教育出版、2005 
5) 遠山啓：無限と連続、岩波書店、1952 
6) Newton別冊：微分と積分、ニュートンプレス、2020 
7) ルネ・デカルト、原亨吉訳：幾何学、筑摩書房、2013 
8) ルネ・デカルト、桂寿一訳：哲学原理、岩波書店、1964 
9) ライプニッツ、下村寅太郎他監修、三浦伸夫訳：ライプニッツ著作集2-数学論・数学、工作舎、1997 
10) ライプニッツ、米山優訳：人間知性新論、みすず書房、1987 
11）石黒ひで：ライプニッツの哲学、岩波書店、1984 
12) 世界の名著30・ライプニッツ、スピノザ、下村寅太郎編、清水富雄他訳：モナドロジー、中央公論社、1980 
13) ニコラウス・クザーヌス、山田桂三訳：学識ある無知について、平凡社、1994 
14) ジル・ドゥルーズ、財津理訳：差異と反復、河出書房新社、1992 
15) ジル・ドゥルーズ、宇野邦一訳：襞、河出書房新社、1998 
16) ベルクソン、平井啓之訳：時間と自由、白水社、1990 
17) ベルクソン、杉山直樹訳：物質と記憶、講談社、2019 
18) ベルクソン、真方敬道訳：創造的進化、岩波書店、1979 
18) アリストテレス：形而上学、岩崎勉訳：講談社、1994 
19) エドムント・フッサール、ジャック・デリダ、田島節夫他訳：幾何学の起源、青土社、1992 
20) 湯川秀樹：本の中の世界、岩波書店、1963 
21) 太田邦夫：エスノ・アーキテクチュア、鹿島出版会、2010 
22) 伊藤哲夫：森と楕円、井上書院、1992 
23) 森田慶一：西洋建築史概説、彰国社、1962 
24) 日本建築学会編：西洋建築史図集、彰国社、1953 
25) クリスチャン・ノルベルグ＝シュルツ、加藤邦男訳：図説世界建築史11バロック建築、本の友社、2001 
26) ルイス・カーン、前田忠直訳：ルイス・カーン建築論集、鹿島出版会、1992 
27) 日本建築学会、『建築雑誌』93,95,96号、1894 
28）ル・コルビュジエ、樋口清訳：ユルバニスム、鹿島出版会、1967 

脚注 
注1）参考文献27) 
注2）参考文献21),pp.81-158、「建築はなぜ四角になったか」の章を参照。 
注3）参考文献20),pp.177-178 
注4）参考文献28) 
注5）参考文献7)、pp.029 
注6）参考文献8)、pp.128 
注7）参考文献22)、pp.154 
注8）参考文献9)、pp.68 
注9）参考文献19)、pp.111 
注10）参考文献5)、pp.51 
注11）参考文献25)、pp.124 
注12）参考文献13)、pp.121 
注13）参考文献12)、pp.435-460 
注14）参考文献14)、pp.269 
注15）参考文献10)、pp.210 
注16）同注8）、pp.28 
注17）参考文献4)、pp.42-45 

Fig.1 プトレマイオスの天動説による宇宙モデル（1524）。出典：Wikipedia 
Fig.2 トルコ、イオニア地方、ミレトスの円形劇場遺跡。撮影：南靖子 
Fig.3 パンテオン（ローマ、118-128）。筆者撮影 
Fig.4 コロッセウム（ローマ、72-80）。筆者撮影 
Fig.5コペルニクスの地動説による宇宙モデル（1543）。出典：同fig.1 
Fig.6ケプラーの法則による、天体の楕円運動と面積速度。出典：日本大百科全書（小学館、1984~1994） 
Fig.7 デカルトによる円運動の考察。出典：『哲学原理』、参考文献8) 
Fig.8 カンピドリオ広場（ミケランジェロ、ローマ、1536-47）。筆者撮影 
Fig.9 サンタンドレア教会（ヴィニョーラ、ローマ、1553）。出典：asianprofile 
Fig.10 サン・カルロ・アッレ・クワトロ・フォンターネ、外観および平面図（ボルロミーニ、ローマ、1638-46）。出典：同fig.1 
Fig.11 サン・タンドレア・アル・クィリナーレ、外観お呼び平面図（ベルニーニ、ローマ、1658-1670）。出典：同fig.1 
Fig.12サン・ピエトロ広場（ベルニーニ、ローマ、1656）。筆者撮影 
Fig.13宮廷図書館（エルラッハ、ウィーン、1723）。出典：WienTourismus 
Fig.14 サイクロイド曲線。出典：monozukuri.sqcd-aid.com 
Fig.15 セントポール大聖堂、外観および平面図（クリストファー・レン、ロンドン、1710）。出典：同fig.1 
Fig.16法隆寺金堂と五重塔（７世紀、奈良）。出典：同fig.1 
Fig.17 キンベル美術館（ルイス・カーン、フォートワース、1972）。出典：同fig.1