On Calculus and Architectural Asymptotics – ircles, Ellipses, and Cycloids
Yasuhiro Minami
1 Encounter of Abstract and Concrete One day in January 1684, as late Renaissance architecture in Italy began to fade away and the Baroque fever wave was ripening across Europe, a new wave of architecture was born. In a London coffee house, there were three men discussing a single topic with great enthusiasm. They were Edmund Harry, an astronomer famous for Halley's Comet; Robert Hooke, a physicist and astronomer; and Christopher Wren, an architect. After a meeting at the Royal Society, the three men shared a cup of coffee and discussed an important issue that would later rewrite the history of science. The orbits of the planets. This was widely known as "Kepler's Law," which predicted that the orbits of the planets would be elliptical according to the universal law of gravitation, which states that the force of attraction is inversely proportional to the square of the distance between them. However, no one could come up with a satisfactory answer to this difficult question during the coffeehouse discussion. So, later that day, Halley, with a single thought in his mind, asked Isaac Newton to teach him. Newton immediately shared his exceptional knowledge of the problem, from which Halley received an innovative instruction and successfully predicted the orbit of Halley's comet. It is interesting to note that 1684 was the year that Leibniz published the world's first calculus paper. At the same time, the mathematical study of the ellipse, the germ of calculus, was clearly connected with astronomy and physics in the field of planetary orbit prediction. The architect Christopher Wren was present (or rather, deeply involved) in the vortex of this historical turning point in the natural sciences. In other words, it was a year in which the procedures and thoughts of "calculus," which are highly abstract, were projected onto concrete physical phenomena, and they overlapped perfectly. The fact that the architect Wren was contemporaneously involved in such a Merkmal turning point in calculus is extremely significant in the history of architecture. Needless to say, architecture has not been unaffected by mathematics since its inception, and to put it in more limited terms, it would not have been possible without an eye to geometry. However, as mathematics became increasingly sophisticated, it began to drift away from the world of concreteness and reality, transforming itself into an abstract logical system that defies intuitive grasping. Descartes brilliantly reversed this trend by discovering analytic geometry, a method of connecting algebra and geometry by means of coordinates, thereby bridging the abstract of logic and the concrete of intuition. But this is not the point we should ask here. What is important is to trace the birth and history of calculus from a historical perspective and ask how it asymptotically progressed to architecture and what it brought about. More specifically, it is to ask what the concept of differential and integral calculus reveals when it passes through architecture. 2 The Circle Celestial Model in Ancient Greece and Rome The discovery of calculus awaits the publication of formal papers by Newton (1642-1727) and Leibniz (1646-1716) in the late 17th century to mark its pioneering origin. However, its origin can be traced back to Galileo Galilei (1564-1642), the father of modern science. Galileo studied the trajectories of falling objects and cannonballs and found that they were parabolas. In other words, he discovered that the motion of physical objects can be depicted as precise geometric figures. But the pioneer who followed Galileo and played the most significant role in the birth of calculus was Descartes (1596-1650). Descartes was inspired by ancient Greek geometry and brought it back to early modern Europe, updating it and discovering a brilliant method that would fundamentally rewrite subsequent mathematical thinking. This was the introduction of the concept of coordinates. In ancient Greece, geometry was the most important field of study. For example, it is said that the motto "He who does not know geometry should not pass through the gates of the Academia, the school founded by Plato. Geometry was considered such an essential field that it formed the foundation of the entire field of study in ancient times. That is why Descartes, inspired by ancient Greek geometry, took up the three fields of "refractive optics," "meteorology," and "geometry" as privileged subjects in his "Introduction to Method" (1637), which developed the core of his philosophy and thought, and pursued them. Here, as he considered various curves, he arrived at the concept of "normal" as an index for describing curves. This is a line perpendicular to the tangent line at a point on a curve, and is almost a pair with the tangent line, which is the key to differentiation. Later, Leibniz and Newton, greatly influenced by Descartes' tangent line, developed it to elaborate the system of differential and integral calculus. Thus, if we trace back the development of calculus historically, we can see the connection between ancient Greek mathematics (geometry) and early modern European philosophy and mathematics, which resonate and correspond with each other across time. Therefore, here, I will first juxtapose the history of calculus in ancient Greece with architecture, and then, while viewing both of them synchronic, connect them to the early modern European period. Looking back to ancient times, calculus has been developed by first drawing on the circle as an ideological figure, and then by overlaying an eye toward astronomy on it. Its prototype dates back to Pythagoras (circa 580 B.C.- circa 500 B.C.). Pythagoras assumed that in the universe, the various planets, including the earth, orbit in perfect circles, and here he created a concentric geometric model of the universe. Slightly later than Pythagoras, Zeno of the Eleatic school (ca. 490 B.C.-430 B.C.) fleshed out calculus from a completely different perspective from astronomy and came closer to its essence. Zeno is known to have invented the paradoxes "Achilles and the Tortoise" and "the flying arrow." All of these paradoxes can be summed up in the problem of what appears at the end of infinite division of "time and space" in line with the motion of objects. In other words, from a different angle from that of Anaximandros (B.C.610 - B.C.546), who posited "the infinite" (a Peiron) as an archetype, the idea/aphoria of "the infinite" was extracted from the actual phenomena of motion. Zeno's view of the continuous and infinite division of time and space is the very procedure of differentiation, which attempts to describe the tendency (tangent) of a phenomenon through the infinite miniaturization of continuous quantities. It is fair to say that the concept of differentiation was already clearly conceived here. Later, in the 4th century B.C., Aristotle (384 B.C.-322 B.C.) proposed a model of the universe as a perfectly stationary state in which the earth is immobile at the center and the moon, sun, and stars move in circles around it. This model was the forerunner of the so-called celestial motion theory and dominated human knowledge for nearly 200 years thereafter. Intersecting with these astronomical observations was the earlier pursuit of integration as a technique of surveying. As far back as the Egyptian period, about 4,000 years ago, we can already see the germ of integration for determining the volume and area of a figure. However, it was the ancient Greek mathematician Archimedes (B.C.287?-B.C.212) who first established the integral technique in earnest for geometric figures. Archimedes calculated the circumference of a circle using the polygonal division method called "method of exhaustion" and succeeded in establishing the extremely accurate value of pi (3.14) in the B.C. period. Indirectly, this was a technique that was an early exposure to the concept of integration, which attempted to flesh out the precise area calculation of a figure. After these pioneering steps, the Roman scholar Ptolemy (circa 83-168), who culminated the ancient Greek astronomy, conceived of a cosmological image of the universe based on a subcircular model as a celestial motion theory (Fig. 1). Here, he defined the distance and configuration between each planet, including Mars, Venus, and other planets, and knitted together an elaborate celestial model that harmonized observational phenomena with a perfect concentric-circle model.

3 Circles and Ellipses in Ancient Greek and Roman Architecture Thus, the cradle of calculus began as far back as 2,500 years ago, when the idea of "infinity" was thought of while connecting the "circle" as a geometric idea and "celestial bodies" as physical phenomena. What about architecture at that time? Needless to say, the development of knowledge in ancient Greece and the cradle of architecture were on the same footing. However, it was still too early to find the intersection of "calculus" and "architecture" in this period. The Parthenon (447 B.C.-432 B.C.) appeared in the 5th century B.C., just as Socrates (470 B.C.-399 B.C.) was working in Athens and Zeno, a pioneer of the Stoics, was creating a mysterious paradox concerning motion. The open-air amphitheaters of Miletus (c. 5th century B.C.) and Priene (c. 350 B.C.), or the amphitheater of Epidaurus (late 4th century B.C.), for example, can be recalled as examples where the "circle" as a geometric idea was explicitly transferred to architecture as a trace line (fig. 2). However, there is no ideological symbolism of "the circle as a geometric figure reflecting the world" in these theaters.

Calculus and architecture had not yet been able to communicate well at this time. Locally, it can be said that the cross section of an order in ancient Greek architecture is posited as a "circle". However, due to artificial operations such as fluting and entasis and their multiplicity, they exist as dots that form the intersection of coordinates rather than as geometric circles, and do not represent the "circle" as an idea. The foundation of ancient Greek architecture was the construction of a homogeneous and endless series of columns, walls, and Cartesian coordinates, with a majestic order rising up, and it existed as a rectangle (and rectangular body) as an artificial ideological representation. Going back to the "origin of geometry" (Husserl) as an idea is in itself a fascinating question. Moreover, as Chuta Ito once argued, if we include the decorative dimension of architectural parts, we can see in Greek architecture not only regular circles and straight lines, but also various developments of complex curves, from which we can find an "archaeology of straight lines and curves" of various complex dimensionsNote 1). However, as long as we look at ancient Greece as the cradle of "calculus" and "architecture," it does not seem possible to extract a clear-cut opportunity for the two to connect. However, from the perspective of human history, it is generally accepted that architecture as a primitive form appeared as curves rather than lines, and circles rather than rectanglesNote 2). Primitive traditional dwellings generally began with circular, horseshoe, or elliptical planes, and it took a long time for rectangular planes to emerge. Simply put, this is because at the beginning of civilization, it was much simpler to fuzzily generate irregular curves than to derive rectangular right angles. In turn, physicist Hideki Yukawa, for example, had the following to say in relation to the "theory of curved space" in the theory of relativity. "Nature creates curves and man creates straight lines...But if we go deeper, we will touch the essence of nature, which is not linear again. Herein lies a problem, especially for the future of theoretical physicsNote3). " Here is a viewpoint that leads to the concept of calculus, which attempts to accurately describe even more advanced curves beyond the point where nature as a curve is replaced by an artificial straight line. Le Corbusier, in his "Urbanisme" (1924), also criticizes irregularly curved streets and argues that straight streets are more humanNote 4). The curves (circles) as a given nature are artificially transformed into straight lines (rectangles), and this is the only way to build up knowledge. In this context, the Greeks, who pioneered a part of human knowledge, launched an aesthetic of straight lines and rectangles that was anti-natural as an opportunity to construct an idea that departed from the circle as an imitation of nature. If so, it is safe to assume that the ancient Chinese concept of the "circle in the heavens" as a symbol of perfect cosmic harmony and the "square on the ground" as a representation of rational human ideals, sharply opposing each other as a watershed separating heaven and earth, was also accepted in Greece. This is a collective knowledge that has been widely shared throughout the world, both in the past and in the present. Therefore, as if to translate the counterpoint between "sun worship" and "earth mother worship," which are said to be the origin of architecture, the following contrasting schematic can be drawn. Circle - Celestial body/Sub-circular model - Nature/Curve - Center / Periphery Square - architectural/ideological model - artificial/linear - homogeneous/repetitive These contrasts and distinctions were, however, brought to a halt by the dramatic space in which the Pantheon (118-128) emerged. This architectural marvel encompassing a 43.2-meter-diameter sphere is a microcosm of perfect harmony, a dome space, which is supported from the outside by a ruggedly circular planar wall structure that is almost impractical in its structural form. The rectangular front colonnade pierces directly into the perfectly proportioned circular dome, sharply accentuating the contrast between the rectangle and the circle. Inside the dome, light pours down from the 9-meter-diameter round oculus on the top of the dome, licking and illuminating the latticework of the latticework that converges toward the apex, and clearly marking time as it shifts (Fig. 3).

This itself is a miraculous reduction and materialization of the celestial model by means of a subordinate circle, which has existed since Pythagoras. It was the emergence of a cosmic model with concentric circles of "man/planet/star/celestial body" that placed the man standing at the center in the world and drew the sky to his hand. It is no mere coincidence that the completion of architecture as a microcosm was completely contemporaneous with Ptolemy's creation of the celestial and cosmic models. Both in time and place, Ptolemy's cosmological model and the Pantheon resonated with each other. Here, the two models overlapped, foreshadowing the advanced development of "calculus" and "architecture" in early modern Europe far into the future. Dome architecture as a microcosm reflecting the universe, astronomy based on a cosmic model centered on the earth, and the circle as the highest form of geometry. These three elements seem to have been joined together in perfect harmony to form a splendid triangle of the Trinity. However, we cannot forget the architecture that cracked the model and foreshadowed the dramaturgy surrounding the calculus that followed. It is the Colosseum (c. 72-80). This gigantic open-air theater, a textbook of classicist architecture, has an elliptical shape with a major axis of 188m and a minor axis of 156m. The proportions are dynamic and full of movement both in plan and in elevation (Fig. 4). The Colosseum was built with the ellipse as a distorted circle for its bloody use as an arena. If so, the Pantheon (circle/sphere) as a symbol of tranquility and wisdom, and the Colosseum (ellipse/inverted cone) as a projection of bustle and dynamics, are ambivalent copies of the celestial model of "circle/ellipse" in the same period, forming an inverted mirror image relationship. Therefore, it can be said that each of them was also connected to the concept of "calculus.

4 Elliptical Celestial Models and the Concept of Calculus in Early Modern Europe The momentum of the intersection of mathematics (geometry) and architecture in ancient Greece had to undergo a long period of abeyance due to the stagnation caused by the "Dark Middle Ages" in Europe after the decline of the Roman Empire. It was Copernicus (1473-1543) who broke free from the blockage of scholastic philosophy and finally broke with the Ptolemaic model of the earth-centered universe, which had remained unshaken for almost 1500 years. By deciphering in detail Ptolemy's data, which had been left behind long ago, Copernicus developed the "Circle of Orbits" model of the solar system, in which the planets revolve around the sun. In 1543, the year Copernicus died, his "On the Rotation of the Celestial Bodies" was published, and the geocentric theory was questioned for the first time (Fig. 5). It is well known that Galileo Galilei reacted strongly to this and supported Copernicus' model, marking a milestone for the geocentric theory.

At this point, it seems to me that we have finally found the ground to shelve the general history of the birth of calculus and summon the fundamental (theoretical) question, "What is calculus?" along the lines of architecture. In general, the usual mathematical definition is that the derivative is "the tangent/trend of a geometric curve" and the integral is "the area/volume of various figures. In fact, as will be discussed below, Descartes and Leibniz, who made tremendous contributions to the development of calculus, repeatedly and unequivocally so stated. They said that the purpose of the derivative is to know the properties of curves, and the purpose of the integral is to know the area of a figure. It is also an indisputable historical truism that the technique of integration was advanced first, the derivative was born later, and Newton revealed their inverted, inverted relationship. However, what I am painfully aware of every time I revisit the common history and general understanding of calculus is the subtle sense of inadequacy surrounding the definition and understanding of the calculus. As is well known, the specific utility of calculus as a technique has been applied in a variety of ways. In fact, in today's complex mix of advanced technologies, there is nothing that is not directly or indirectly undergirded by the techniques of calculus. The techniques of calculus are so highly compatible with minimization, efficiency, optimization, and the concept of time that they are constantly running alongside and cohabiting with technological advances. Highway design as an operation of curvature, maximum efficiency of generators, car design of fluidic forms, satellite speed calculations, CT scan design, and probability theory in financial engineering, to name just a few. It is needless to point out once again that this method is also indispensable for seismic isolation technology in architecture. However, once we turn our eyes away from such real-world applications and question the meaning of this concept, we are instantly bewildered by the lack of thought. What does the discovery and development of the concept of calculus mean in metaphysical terms? And beyond that, what principle implications does calculus have for architecture? The model of the universe as a geocentric theory, which Copernicus developed heuristically at the dawn of the Dark Middle Ages, however, still traced the motion of the heavenly bodies by means of circles. It was the astronomer Kepler (1571-1630), referring to Copernicus' findings, who redescribed it by ellipses, thus raising the resolution of reality reading to a whole new level. Kepler learned the art of observation from his mentor Tycho Brahe, and by studying the complex movements of Mars, he arrived at the famous three laws. The three laws are as follows (Fig. 6).
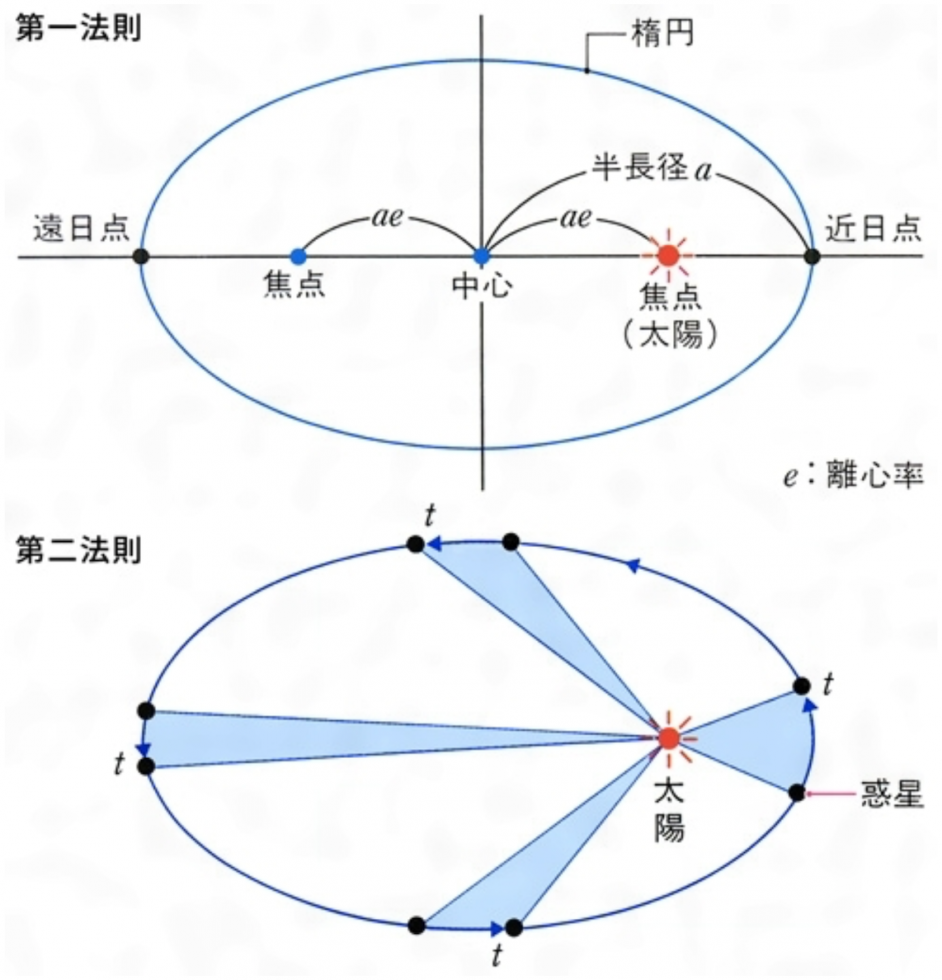
The first law: the orbit is not a circle, but an ellipse with the sun as the focal point. Second law: The area velocity of planetary motion (the area that the line segment connecting the sun and the planet passes through in a given time) is constant. Third law: the square of the orbital period of a planet is proportional to the cube of the semi-major axis of the ellipse (the average distance between the sun and the planet). This was, indeed, a revolutionary discovery. This is because it dislocated the "harmonious and uniform cosmological model = circle" as a simple human desire, drew on the "ellipse," and accurately read through the real phenomena. Furthermore, Newton miraculously opened the door to the simultaneous conception of "universal gravitation" and "calculus," which are the cornerstones of modern science. Kepler's definite law of area velocity was nothing other than the mechanical view of "the balance of the universal gravitation force by the sun + the motion trajectory of the ellipse. Thus, the shadow of the ellipse engraved by the Colosseum was transferred to the modern era, skipping over the millennium. Here, the history of "calculus" and astronomy parted company for a time. Galileo and Descartes, Newton and Leibniz, bridging astronomy and geometry, moved the stage of thought from the universe that covers the heavens to the microcosm of their own thought. Galileo, the "father of modern science," discovered that the trajectory of a thrown object can be described by parabolas and that natural phenomena/gravity can be defined geometrically, as he repeatedly examined motion and fall. Galileo's laws of motion and geocentric theory had a great influence on Descartes, who was living in the same period. This led to an important opportunity for the birth of calculus. Descartes, in his "Geometry," published in 1637, wrote "Even the most complex lines are drawn by a single continuous motion, or by a multitude of motions which are so interconnected that the last is completely regulated by the preceding motionsNote5). " This is literally the very definition of differentiation, which considers various curves as "motion trajectories" and then tries to derive their tendencies/tangents. Descartes, who was inspired by the drawing problems of geometry in ancient Greece to develop mathematics, repeatedly states in this book how to define and draw curves precisely. Beyond that, he also tries various methods of drawing complex curves precisely, claiming that in ancient geometry, the limit was limited to understanding "conic curves by Apollonius (ca. B.C.262 - B.C.190)," such as hyperbolas and ellipses. Descartes discovered a way to plot the normals of various curves at arbitrary points. For Descartes, knowing curves was the core of his reasoning to penetrate the mystery of how the world came to be. Descartes' considerations were limited to curves because he had not yet arrived at the concept of tangent lines in differentiation and described curves by normals orthogonal to tangents. On the other hand, Descartes saw that the circular motion of an object was impregnated with vectors in the tangential direction (Fig. 7). He said of the motion of an object released from a circular motion, in his "Principles of Philosophy," that

"It is that everything in motion is destined to move in a straight line in a certain direction, and never curvilinearly, at each moment that can be marked during the motionNote6). " This recognition by Descartes, which suggests the tangent line of a curve (circle), corresponds precisely to Galileo's law of motion, which attempts to define the parabolic motion of an object by dividing it into two parts, "gravity and direction of motion. Here we can see the excellent fusion of geometry as the drawing of curves with the laws of motion as a physical phenomenon. Thus, Galileo's method of natural observation was translated into the pursuit of pure geometry by Descartes, and through calculus, events and concepts, facts and ideas were perfectly superimposed. 5 Ellipses in the Early Baroque Period and Leibniz's Calculus Europe was in the midst of a transition from the Renaissance to the Baroque period, when the "circle," a harmonious superposition of astronomy and geometry, began to slide off the face of the earth and transform into the "ellipse," which was full of movement. A pioneering example of the ellipse in architecture and the city is the Piazza del Campidoglio (1536-47, Rome, apart from the architecture) by Michelangelo (1475-1564) (Fig. 8).

This pioneering Baroque-style piazza reads the site's inverted trapezoidal shape into a huge, well-balanced ellipse, in the center of which stands the equestrian statue of Marcus Aurelius. Here, the effect of perspective is emphasized through a strict symmetrical arrangement with the central axis extending from the hill to the city, taking the vista into account. At the same time, the grand staircase and elliptical plaza of the gradually widening approach create a movement and flow that lures people in. This gives it a centripetal perspective that consolidates the classical façade that surrounds it on three sides and transforms it into a straight line along its long axis, giving it an ambivalent effect. Furthermore, the floor incorporates a star-shaped pattern of twelve angles, creating a dramatically different sense of space from the static circle motifs often seen in Renaissance architecture. In contrast to the ellipse as a square, one of the earliest examples of the ellipse as architecture is the church of San Tandrea in Via Flaminia (Rome, 1553) by Vignola (1507-1573) (Fig.9). This is a small building with a simple rectangular top surmounted by an elliptical cylinder inscribed with an elliptical dome inside. The rectangular plan and the elliptical ceiling are combined, and the edges of the rectangular cylinder are redundant, creating a curious volumetric effect. The most interesting point is that the ceiling as a vaulted ceiling is expressed by an ellipse. In other words, the ceiling itself can be read as an allegory suggesting the sky/orbit as an ellipse. Furthermore, it should be noted that the lower rectangular body itself, which is circumscribed by the ellipse, is arranged as an enclosure of tangent lines, which are derivatives of the ellipse. Vignola's architecture represents the geometrical concept of the ellipse in a simple, and therefore, in a sense, extremely pure form. If so, it is not difficult to imagine that this pioneering small work had a great influence on the later master architects of the Baroque period.

However, the relationship between Baroque architecture and the ellipse is not simple, and their establishment and development do not necessarily coincide. In his discussion of European elliptical architecture, Tetsuo Ito notes that the elliptical space corresponds to the Mannerist period from the 16th century onward. The establishment of the elliptical space was essentially a compromise between the circular space of the Pantheon and the space of the basilica, the original space of the church, in the context of the "Counter-Reformation" against the Reformation that took place in the northern countries. In other words, according to Ito, the ellipse in architecture emerged as a fusion of the circle (concentrated form) and the rectangle or Latin cross (basilica form). Furthermore, it should be added that many elliptical motifs in the Baroque were derived as a result of mediating between the straggle of straight and curved lines by reading the context of the place, and were also graphic models bridging the conflict between the city and architecture. Since Kepler first introduced the three laws of the ellipse in 1609, Vignola clearly embodied the geometric motif of the ellipse in architecture much earlier than that. It was an accelerated Mannerism, so to speak, in the pre-Baroque period, since it anticipated the fashion for the ellipse that would eventually overtake the Baroque period by nearly a century. Thus, the complex of concepts such as the ellipse, celestial navigation, universal gravitation, architecture, and calculus were beginning to form a complex magnetic field of knowledge that sometimes jumped back and forth between them. After all these cradles and trials and errors surrounding calculus, in the middle of the 17th century, there came a period of "marvels" that fundamentally changed the history of science: Newton's three great discoveries in 1665-1666: the Law of Universal Gravitation, the Calculus, and the Theory of Light. Influenced by Galileo and Descartes, Newton mastered the most advanced science in just a few years and arrived at his miraculous discoveries. But Newton, a cautious man, did not publish those results for a long time, and it was not until 40 years later, in his Theory of Calculus, published in 1704, that he formally published calculus. Before that, in 1687, Newton published what is considered the most important book in the history of science, Principia, in which, perhaps intentionally, he did not use the concept of calculus. Leibniz, who came up with the idea of calculus in 1675, was the first to introduce calculus to the world in 1684, ahead of Newton. This led to the coffeehouse discussion at the Royal Society in 1684. Because of this convoluted history, a long and bitter dispute continued between Newton and Leibniz over the true originator of calculus. It is said that Leibniz, who was defeated in the dispute, died of a broken heart. However, both men are now recognized as the discoverers of calculus. In other words, calculus as a mathematical concept was discovered in 1665 through the accidental and contemporaneous work of Newton and Leibniz, and by 1704, when the time was ripe, it was rigorously defined and became the full-fledged shared knowledge of humanity. At this point, the basic concepts of calculus were completed in one fell swoop and applied in a variety of ways that remain largely unchanged today, including the symbolic method devised by Leibniz. The elaborate model that these two men constructed was, therefore, of an extremely high degree of perfection. However, Newton and Leibniz had different approaches to calculus. Newton defined calculus from a physical approach, based on motion, its velocity (tangent), and its flow rate (area). In contrast, Leibniz explained calculus geometrically using the micro-triangle dy/dx and the strip-like miniscule rectangle ∫ydx. The results they arrive at are the same, but the difference in their approaches expresses the style of their solution methods. In a manner of speaking, Newton's method was calculus as dynamics/physics, whereas Leibniz's was statics/geometry. As can be seen from these differences, both universal gravitation and calculus, which Newton discovered during his "years of wonders," were extremely beautiful and simple principles derived by abstracting real physical phenomena. What is interesting to note here is that Newton's thinking is such that he, so to speak, deconstructed the concepts of "absolute space and absolute time" that he himself had defined. In other words, he redraws space-time (the assumption of absolute coordinates), which defines physical motion, by means of calculus, which is the trajectory of motion. This is because mathematical tools such as calculus and non-Euclidean geometry by Riemann, Lobachevsky, and others would eventually prepare the theory of relativity that would shake 20th century science, and lead to the concepts and systems of relative space and relative time. Newton's concepts of absolute space and absolute time were established by Newton himself, and at the same time, they were dismantled from the inside by Newton himself (calculus). In fact, Leibniz strongly rejected Newton's concepts of absolute space and absolute time, defining space and time as "the order (arrangement) and relations of things and events. Leibniz describes space and time as follows. "Time tempus is the order of the existence of things that do not exist at the same time. It is therefore the general order of change, in which the type of change is not taken into account. Spatium is the order of coexistence, that is, the order of the existence of things that exist simultaneously with each other.Note8) " Based on this recognition, Leibniz invented calculus as a concept of micro- and maximalism in a non-contradictory form. What is important is the meta-level issues that emerge from this flow and development. The concept of calculus is literally defined as "finding the tangent of a curve or the area of a figure," but what these concepts are aimed at is the question of the existence of the form of "time and space," which has been a great mystery since ancient times. Calculus, therefore, supports the definitions of space and time from behind the scenes. Leibniz's attempt to describe space-time forms in terms of relations is precisely Leibniz's attempt to use calculus to outline an abstracted "non-existent object" such as a figure from an angle other than geometric clarity. In other words, it is not a predicate definition of "a priori transcendentalist form" (Kant), for example, to answer the questions "what is time" and "what is space? Rather, it projects the concept of space-time itself into a figure, and then shifts the question to "the mother of relations and order," which is "the tendency of curves/the infinite set of infinitesimally small things. And here, I think we can find an opportunity to connect calculus, which at first glance appears to be a special mathematical technique, to architecture as space. That is why Gilles Deleuze, for example, connected the Leibnizian monad with the informality of Baroque architecture, and tried to depict space through the composition and relationship of "folds". In other words, instead of grasping the origins of architecture through the dichotomy of "volume as a physical object/space as an imaginary object," he may be trying to depict it again as "a synthesized form of micro-sections of ripples. In considering calculus as a concept, we should recall Husserl's "The Origin of Geometry" and ask once again why it did not deal (in a kind of thorough and deliberate way) with the concrete issues of geometry itself. Husserl, when he problematized the origin of geometry, did not refer to geometry itself at all, such as the history of the parallel axiom in Euclidean geometry. The core of what is being discussed there is a reading of the historical determinants of the inevitable construction of the system of knowledge, why geometry as a discipline was constructed as it is today (and why it was not in any other form). In other words, Husserl is there trying to ask fundamentally what we might call the "institutionality of the discipline," why geometry, the framework of knowledge (which represents the whole discipline), developed in this way and what it means for human knowledge. Therefore, Husserl's question, which seems to bypass geometry itself, appears mysterious to the reader. That is why Jacques Derrida reads this essay by Husserl with remarkable resolution, stating that geometry "constitutes an object when it is recaptured in its fundamental purity," and fundamentally questioning the meaning of the discipline of geometry as it emerges in its inherent contoursNote 9). This, in turn, leads to the question, "What exactly is the object of mathematics (geometry), and what is it trying to do? Russell, for example, responded to such questions about mathematics as follows. "Mathematics is a science in which we do not know what we are talking about, nor do we know whether what we are talking about is true or notNote10). " This famous statement about mathematics has certainly brought a sense of clarity to many people. What we see when we accept such a statement and then superimpose an architectural class on calculus and geometry is the following. That is, calculus is asymptotically close to geometry by virtue of its ambiguity that connects concrete physical phenomena and abstraction as an idea. Calculus is the semblance of an externalizable logic that fleshes out the mystery of concrete phenomena. In other words, it is a conceptual fluctuation that appears at the end of the asymptotic approach to the ungraspable. It is at the same time geometry and not. In other words, it is one of the procedures to deconstruct the constructiveness of the discipline that has been self-evident since ancient times. It is a simple technique to decipher the entire composition of the world (and for architecture, the dichotomous totality of <volume/space>) in one fell swoop by means of unrecognizable infinitesimally small slices, a miraculous leap where the very small is directly connected to the very large. The infinitesimally small correctly describes the entire world to infinity. With this, we cannot help but recall Mies van der Rohe's quote, "God is in the details". Mies' words are aimed at the parts of architecture as objects. However, when we superimpose the concept of calculus on architecture, we are in close proximity to something that goes back and forth between the two, which are intricately defined by the distinction between "thing (real) and space (imaginary). In other words, the procedure of questioning the boundary conditions between objects and space itself may rise up as the intersection of architecture and calculus. In fact, we can find many elliptical motifs, one of the model figures of calculus, in Baroque cities and architecture. However, they are sometimes ellipses as objects, spaces, enclosing squares, or iconic representations, traversing various dimensions and phases. It suggests a conceptual expansion that cannot be accommodated by simply stating that "the Baroque has the ellipse as its main motif. It is as if, by passing through the concept of ellipses, their physical state of existence has receded into the background. It seems to function as an invisible measure that dissolves and traverses the boundary between the real and the imaginary, describing their respective properties. Descartes, for example, understood it in terms of the concept of "extension" as an infinitely expanding coordinate system. Calculus, however, further enhances the space-time dimension of the "extension" and attempts to depict the movement itself. It is an amorphous notation that attempts to depict the formation of things as a manifold of superimposed static and dynamic states. In this sense, calculus is an excellent mathematical tool for accurately describing physical phenomena based on the composition and behavior of things, and at the same time, it can be said to point to "the twist and outside of concepts" that opens up a "dimension as persistence," away from the framework of dichotomous recognition of the real and the virtual. 6 Elliptical Space in Late Baroque Cities and Architecture The discovery and development of calculus in mathematics and physics coincides beautifully with the "elliptical" competition that took place in the architecture of the Baroque period. One of the most representative architectural examples is San Carlo alle Quattro Fontane (1638-46, Rome) by Borromini (Fig. 10).


Considered one of the greatest masterpieces of Baroque architecture, this small church is the most vivid expression of Borromini's architectural characteristics, described as a "whole with complexity" (Giedion). According to Christian Norberg-Schulz, no other building has been subjected to such repetitive plan analysis as this oneNote 11). It achieves an unusual density of design within the extremely demanding corner site conditions, from the wavy façade to the complex ceiling composition, to the detailed design and control of the line of sight. The result is a dynamic space in which the essence of the condensed baroque has blossomed in a single stroke, thoroughly crafted down to the smallest detail through a form that is full of intense emotion. The centerpiece of the building is the elliptical hall in the center. The originally rectangular plane is transformed into an irregular cross shape, which is transformed into an ellipse as it moves upward, and various lattice figures are inlaid into it to create an extremely unique and complex flat section. The ellipse employed here is precisely created by adjoining two regular circles and connecting them with a curve. In other words, an intermediate form between a circle and a rectangle is derived, and in the severe conflict between site and function, an ellipse that is almost a super-ellipse is derived, as if it were a deformation of a rectangle. The building also has a large elliptical medallion symbolically attached to the top of the facade, as if to forcefully tie the distorted facade together, and one can read a confident preoccupation with the ellipse. It was an architecture that expressed its own (and the era's) worldview and architectural vision with surprisingly high density on an extremely small site, and in keeping with the aesthetics of the indefinite, the dialectic of the part and the whole blossomed through the ellipse. Another representative of the ellipse in the Baroque period is the church of San Tandrea al Quirinale (Rome, 1658-1670) by Borromini's rival, Bernini (Fig. 11). Located only a few hundred meters from Borromini's church of San Carlo, this church is the work of Bernini, who was proud to call it his masterpiece. Due to the unfavorable site conditions, the entrance and main altar are placed on the short axis, using the ellipse as a transverse axis, and the elliptical canopy, which is stretched out, creates an elegant atmosphere. The elliptical canopy, which stretches out, creates an elegant atmosphere. The spatial effect of the ellipse, which is a counterpoint to Borromini's San Carlo church, is expressed in a highly refined form both inside and outside. The symmetry of the overall composition and the skylight at the top of the cupola are reminiscent of a distorted pantheon.


In Bernini's architecture, too, the figure used is not a strict ellipse, but a pseudo-ellipse. The curves are more graceful and well-defined, giving a strong sense of neat geometric proportions. Bernini designed this building without compensation out of deep resonance with his faith in the Society of Jesus. It is an interesting episode that a masterpiece representing Baroque architecture was created by a volunteer, even though Bernini was one of the leading architects of his day. A work that has a strong morphological analogy with Bernini's small buildings is St. Peter's Square (Rome, 1656-67), also created by Bernini (Fig. 12).

St. Peter's Square consists of an inverted trapezoid in front of the cathedral combined with an ellipse, and the overall outline resembles that of a posterior vault. However, due to technical problems in construction, the ellipse here is actually designed as an ellipse by partially superimposing two different arcs, and is strictly speaking a pseudo-ellipse.And the inverted trapezoid in front of the cathedral was modeled after Michelangelo's Piazza del Campidoglio. To it, Bernini added a vast elliptical square consisting of 240 meters wide. This was Bernini's attempt to relate the cathedral to the square by imitating a man with his arms spread wide, and it would be possible to read into it an anthropomorphism connecting heaven and earth. However, it is said that Bernini's elliptical square was originally inspired by the ellipse of the Colosseum, and two ellipses, the Campidoglio and the Colosseum, are reflected in it as a tribute to the Colosseum. In addition, by arranging the ellipses in the direction of the minor axis, it creates an expanse of view orthogonal to the central axis, a composition that bears a strong resemblance to the church of San Tandrea al Quirinale. Furthermore, the two locations that serve as the pseudo-focal points of the ellipse are localized as the "center of the columns" (centro del colonnato), and from this point of view, all four rows of columns overlap, creating the illusion of a single column. This suggests the center of the doubled ellipse and creates the simultaneity of "the extension of the central axis and the centripetal nature of the enclosure" and "the expansion and contraction of the line of sight," skillfully giving the entire square an ambivalent character of liberation and closure. In this way, the Baroque motif of the ellipse reached its zenith in the realization of St. Peter's Square. And at the very time that the architect Bernini was working on the creation of this vast curved elliptical square, Newton and Leibniz were perfecting and refining the concept of calculus through the analysis of curves. Inadvertently, the concepts of architecture and calculus were in synchronic traffic. 7 Nicolaus Cusanus and the Monad as a Calculus Model Thus, from the multilayered intersection of the dimensions of astronomy and theology, geometry and motion, we see that the circle shifted to the ellipse and the calculus was created. Since ancient times, the circle has been an ideological figure (or graphic idea) that symbolizes variously perfection and perfection. The reason why geometry was most important in ancient Greece, led by Plato, was that it could most explicitly indicate the Idea as a concept. For example, the idea of a circle or equilateral triangle as a geometrical idea that does not exist in reality, or the idea of a straight line extending to infinity. The circle as a figure, in particular, is a superlative figure that connects and represents astronomy and theology, the infinite and the perfect, without excess or deficiency. That is why, since ancient times, from Aristotle to Copernicus, the circle/sphere model has been the unshakable basis for the existential localization of man and the standard for depicting a perfect and matchless worldview. The calculus established by Newton and Leibniz has brought about the complete dissolution of such a model in one fell swoop, but in fact, such an opportunity was secretly conceived in medieval Europe. It is well known that Leibniz was greatly influenced by the medieval philosopher Nicolaus Cusanus when he developed calculus. However, the ideas of Cusanus, while being in close proximity to the ideas of Neo-Platonism, were later jumped upon by Giordano Bruno. In the Middle Ages, Cusanus and Bruno received the concept of "infinity" from Neo-Platonism and tried to develop a way of thinking that projected it into the real world. As a result, Bruno proposed a theory similar to the geocentric theory from an astronomical point of view, which was regarded as heresy, and he was eventually burned. But let us leave that aside and look at the ideas of Cusanus, who foresaw the concept of calculus by hand. More than 200 years before Newton and Leibniz conceived of calculus, Cusanus, in his "Learned Ignorance," said through mathematical allegory "The greatest cannot be opposed to anything, and the greatest is the least as it is. Therefore, the infinite One is the One who implies all things and unites all thingsNote12)." This phrase of Cusanus' was, of course, developed in accordance with the theological imperatives of the Middle Ages, but it is nothing short of amazing that it is almost precisely the prototype for the definition of calculus. Cusanus constructs a way of perceiving the world by combining mystical thought with mathematical thought. Relying on geometry, he defines the circle, the sphere, and the triangle as perfect figures, from which he derives the idea of infinity by thinking of "infinitely large circles" and "infinitely large triangles. It is necessary to note the narrative of the unity of the "greatest" and the "least" that is suggested here, and the allegorical recognition of the "union of the one and the infinite" that "all things are in all things" derived from Anaxagoras. This is because it corresponds almost precisely to the mathematical definition that the whole of a curve is grasped by means of the derivative (minima), and vice versa, the integral (maxima), which measures the whole from its parts. Moreover, the "monad theory" constructed by Leibniz owes the invocation of the word monad to Bruno via neo-Platonism. In his Monad Theory, Leibniz says the following. "A monad is a single entity that makes a complex. Single means having no parts. The monad is the true atom in nature. In a word, they are the elements of the whole forestNote13). " Needless to say, when Leibniz speaks in this way, the "atom" here should never be superimposed on the concept of atomism by, for example, Democritus and others. The monad Leibniz speaks of should not be conceived as a homogenized collection of microparticles (i.e., as a spherical material particulate), contrary to the image that the word "monad" might bring. It is a residual concept of "change/persistence/transportation" that is difficult to grasp, and that is what the calculus is all about, and that is what it is all about. Therefore, Leibniz's theory of monads should be read as an alternative theory of calculus. The monads he refers to here are "windowless," "all different from each other," "constantly changing," and "containing all in one." Each monad represents the world in its own way. Within the smallest one is encompassed the greatest multitude. In other words, the smallest is the largest, and the idea of the infinite is inverted there. Needless to say, Leibniz's thought is in mirror-image correspondence with the mystical thought of Cusanus. Therefore, calculus is more than just a mathematical technique; it is a circuitous procedure for recognizing the world. It is a radical world-recognition technique that attempts to read the essence of the world from the strength of its deflection once the world is distorted. Leibniz depicted this allegorically through the model of the monad. Leibniz wrote the first draft of his monad theory in 1714, but he was later very interested in the architecture of the Court Library (1723, Vienna), designed by the architect Fischer von Erlach(1656-1723) (Fig. 13). Here we see an interesting resonance between calculus, ellipses, and architecture. The Court Library by Erlach, who had studied under Bernini, is a masterpiece of Viennese Baroque architecture, and its central hall with its ellipse and dense ornamentation is the subject of the space. Monad and baroque, ellipse and folds, were Leibniz's concept of a series of connected beads. If so, Leibniz probably saw the architecture of his time (and the geometry and trajectory of movement it suggested) as a metaphor.

This is why Deleuze read Leibniz's monadology through Baroque architecture, depicting it not as discrete particles, but as fractally expanding and contracting "folds" whose boundary conditions are indeterminate. Deleuze's concept of the baroque house, therefore, was not merely a rewriting of the material/spiritual dichotomy, but an attempt to describe the totality of the flow and duration of the unimaginable and uncontrollable in the form of an unimaginable monad. Early in his career, Deleuze developed a generous metaphysics of "difference and repetition," in which he spoke of the possibility of potency, of the idea being infinitely differentiated by means of calculus. Calculus is taken not only as a description of motion, but also as an intensity that causes motion to occur. Deleuze said about the calculus. "The derivative is indeed pure power (puissance), and likewise the differential relation [dy/dx] is the pure element of potencyNote14). " Differentiation is not a static description of a phenomenon, but is itself a trace of dynamics intervening/inserting itself into the world. Already in the early stages of his work, Deleuze superimposes on calculus the concept of "folds," the predecessor of the folds. From this trajectory of Deleuze's thinking, we can see how Leibniz's theory of the monad is superimposed on the concept of calculus/infinity via the metaphysics of "difference and repetition. As already mentioned, Leibniz, in his "New Theory of the Human Present Intellect," points out that space is relation and order, not absolute space, which is an infinite whole, and then says, "One of the most important of the relational conceptions is that of identity or difference"Note 15) .One of the important things that the term "differentiation" here focuses on is time and duration, and the critical difficulty of grasping them. This is a distant connection to Zeno's paradox and an asymptotic one to Bergson's recurring problematization of "consciousness and time as pure duration that cannot be spatialized. How can we posit the "here and now," which cannot be determined, at the tip of the idea of infinitesimals and infinitesimals? This is the core of the problem system of calculus, which leads to the recognition of time and duration. However, that is not what I want to ask here. In questioning the relationship between calculus and architecture, what we need to look at here is the history and meaning of what is found in the dialectic of stillness and motion when time is superimposed on geometry. And this question will lead us to the interest of Christopher Wren and his colleagues at the beginning of this article. 8 Hellenes of Geometry, Cycloidal Curves Along with the discovery and development of calculus, there is a figure that fascinated many mathematicians and philosophers at the dawn of modern science. It is the cycloid curve (Fig. 14).
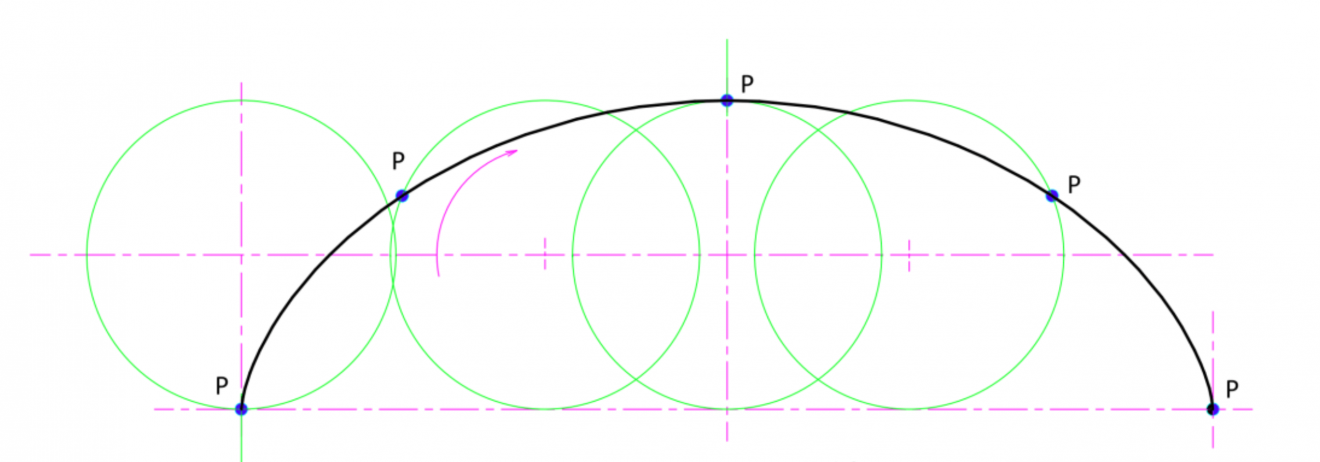
A cycloid is the curve of the trajectory drawn by a point on the circumference of a circle when the circle is rolled on a straight line. Galileo, Descartes, Leibniz, and other famous intellectuals all showed interest in this curve and repeatedly challenged the difficult problems related to it. For this reason, the cycloid curve was called the "Helene of geometry" because it was compared to a beautiful woman in Greek mythology who fascinated many people. This is because, despite the simplicity of the principle of the curve, it has extremely fertile and essential properties concerning the phenomena of reality, which no one has been able to elucidate successfully for a long time. This curve, which appears to be a wave with singularities, contains within it the multilayered properties and problems that are at the core of calculus. Finding its area, arc length, tangent line, and center of gravity became outstandingly difficult and drove every rare genius. It is said that Nicolaus Cusanus was the first to focus on this cycloid. Cusanus focused on the cycloid while working on the circular product problem (the problem of squaring a circle), one of the three major drawing problems of ancient Greece. There are various theories on this, and although nothing definitive is known, it is very likely that he was interested in this curve, as can be inferred from Cusanus' writings, in which he continued to think about infinity and curves, and circles and motion. However, in Cusanus' thought, it was only a suggestion of an image, and the development of a rigorous theory of cycloids, with mathematics and physics as a preliminary picture, had to wait for Galileo's emergence. The cycloid as a mathematical curve was discovered and named by Galileo in 1599. It was also called a roulette at the time, a term meaning derived from a circle. It is possible that, perhaps intuitively and unconsciously, the cycloid curve itself was recognized from very early in the history of mankind as a frequently occurring motion phenomenon in reality. It is a wheel. This is because the phenomenon of moving a circle on a straight line is precisely the trajectory of a wheel itself. The world's oldest wheels have been excavated from the Mesopotamian and Indus civilizations around 3000 B.C., which means that humans already had cycloids in their inventions and activities at the origin of their civilization. Galileo pursued the idea of using the swing of a pendulum in a clock and arrived at the isochronism of the pendulum. In other words, the period of the pendulum is approximately constant, regardless of the width of the swing or the weight of the pendulum. This was made more rigorous by Torricelli, a pupil of Galileo, and Huygens, who was obsessed with clockmaking. Torricelli published his "Geometric Works" in 1644, in which he mentions the properties of the cycloid curve. Huygens also devised a physically rigorous pendulum clock by modifying Galileo's pendulum theory, and in 1657, he discovered that it was the cycloid curve that guided it. This was literally called the cycloid pendulum, and the pendulum clock was born in 1673. By transforming Galileo's pendulum curve as an arc into a cycloid curve, he precisely linked geometry and physical phenomena. Thus, the engineering imperative of the invention of the pendulum clock and the mathematical curve of the cycloid curve are beautifully superimposed. On the other hand, the quest for the mathematical properties of this curve attracted renowned philosophers and mathematicians, and it stood as a historical conundrum that spanned the centuries. First, Galileo, Descartes, and other scientists tackled one after another the problem of quadrature to find the area bounded by a cycloid and a straight line. But they failed at every turn. Eventually, in 1634, Roberval succeeded in finding the area and proved that the area is three times that of a circle. It is said that Descartes himself was chagrined by Roverval's proof, which shows how fascinated they were with cycloids. Later, the method of drawing a tangent line to a cycloid also became a hot mathematical problem, and likewise, many intellectuals repeatedly made mistakes. After much trial and error, Fermat discovered the tangent method for cycloids. One night in 1658, the 36-year-old Pascal suffered a severe toothache, and in order to forget the pain, he spent the whole night concentrating on the various problems of the cycloid. As a result, he solved various difficult problems surrounding cycloids and published a treatise that would become a popular masterpiece in the history of mathematics. These problems included the area of a cycloid, the determination of its center of gravity, and the volume and surface area of its rotating body. The paper was published under the pseudonym "Dettonville" by Pascal, who was away from the secular world at the time, and his outstanding discoveries shocked the world. This paper would later have a profound influence on Leibniz and lead to the discovery of calculus. In fact, references to cycloids appear repeatedly in Leibniz's calculus-related mathematical treatises. It was a privileged figure that intensively represented the mysteries of calculus, and it was a magnet in the minds of the intellectuals of the time. To Pascal, who made a revolutionary contribution to the elucidation of the cycloid curve, Huygens, Fermat, and other cutting-edge researchers at the time were sharing their ideas and research results. One of the most important of these was the architect Christopher Wren, who was mentioned at the beginning of this article. In 1658, Wren succeeded in calculating the circumference of a cycloid and formally proving that it is four times the perpendicular of a circle. This was the famous law known as "Wren's Theorem," which came as a great shock to the people of the time. Even Pascal could not solve it, and Huygens went out of his way to praise it in a letter of the time, saying, "This is a wonderful discovery. The calculation of the circumference of a curve was such an extremely difficult problem before the discovery of calculus, and it had been troubling many researchers. After 1661, immediately after the discovery of the theorem, Wren became a member of the planning committee for the reconstruction of St. Paul's Cathedral in London, and it took 35 years from the start of construction in 1675 to complete the cathedral (Fig. 15). In its interior, this neoclassical architecture with Latin crosses is reminiscent of the sumptuousness of the Baroque style, but without traces of Baroque fluidity, elliptical motifs, or irregular shapes. Morphologically, it is a series of domes and arches, each consisting of a series and repetition of regular circles, and when viewed in plan, it is clear that the circle and the arc are the basic units of the overall composition in an autochthonous manner.

Wren, who understood the characteristics of the cycloid best, may have arrived at the creation of a space impregnated with movement while returning to the form of the circle by reducing the flow from circle to ellipse and from ellipse to cycloid, beyond the complications caused by the Baroque and Mannerism that swept the age. 9 Calculus as a spatial description The cycloid curve thus became the focus of science, involving not only mathematicians of the time but also philosophers and architects, because it connects geometric ideas and actual events in various dimensions in a way that seems like a miraculous coincidence. And this, in turn, led straight to the heart of the discovery and development of calculus. In general, cycloids are described by two major physical properties: the first is the property of fastest descent, discovered by Johann Bernoulli in 1969, which presents a problem. The question is what is the shape of the curve that reaches its lowest point in the shortest time, assuming that a quality point sliding down a certain curve descends with zero initial velocity. The solution was none other than the cycloid curve. Newton and Leibniz also entered this problem, each arguing that he solved the problem first. The other is a property discovered by Huygens called isochronous curves. This means that a quality point on a cycloid will have a constant time of descent regardless of the position of its starting point. The elucidation of this property led Huygens to create the aforementioned cycloidal pendulum, which made a significant contribution to the invention of the accurate mechanical clock. These two properties of the cycloid curve indicate that The cycloid, which was derived from the extremely simple procedure of circular motion on a straight line, was in fact a special curve in which the laws of motion were latent, frozen in motion, so to speak. In other words, the cycloid does not define a geometric figure as a static image, but rather as a representation of drawing in relation to motion (or rather, only in relation to it). And these features of the cycloid were precisely in response to Leibniz's relation of the geometric figure to motion. In a mathematical treatise published in 1695, Leibniz said "Motion itself can be treated geometrically, as long as we do not consider causes or potentia. For a line, or indeed any figure, is a trace of motion. As I see it, once the laws of motion have been established, determining time, speed, and path is a purely geometric matter Note 16). " The cycloid, a geometrical curve, is precisely the curve that stands in for the cessation of motion and stillness (the synthesizing of ideas and phenomena) that emerged from such a recognition by Leibniz. Indeed, the Idea of which Plato spoke is said to have derived its model from the perfect figures of geometry. In addition, it is needless to recall that one of the most important problems that Aristotle, who slid Plato's system of problems, addressed was how to grasp motion. How to relate geometry, which posits ideas (as a possible state), and motion, which is a physical phenomenon (as a reality), and how to describe them simultaneously, has always been a major problem for human knowledge since its inception. The cycloid curve existed as one of the points of arrival. It was based on the circle as a symbol of a completely static idea/astronomical cosmological model, but by moving it, it drew geometry as dynamics/movement and gave rise to the concept of calculus, which is connected to the infinitesimal and the infinite. As we have seen, the circle, ellipse, and cycloid as geometric figures connected ancient Greek and post-medieval knowledge via astronomy and physics, and precisely matched ideas and reality as if they were cast in a mold. In the process of transition from the circle to the ellipse to the cycloid, the architecture, which had always existed as the materialization of ideas, was projected with its iconography and forms, and the response and drama of space were confirmed in various ways. Elementary geometry then developed into elliptic geometry (geometry that considers spherical properties), differential geometry, and the manifold problem that is its central theme, triggered by the development of calculus. This is a field that attempts to clarify the properties of surfaces and curves in various mathematical spaces, and is concerned with "distorted spaces" and "curved spaces," and with figures and spaces that allow the simultaneous existence of various local coordinate systems. The aspect of "each existing differently at the same time" overlaps with the image of each architecture as having its own spatial aspect (individual coordinate system). This eventually leads to the theory of relativity, which deals with the distortion of space-time due to gravity. It is true that the definition of the term "space" in architecture is much less rigorous than those in mathematics and physics. However, it can be said that the complex state of architectural space, which is guaranteed to be a physical phenomenon, has the potential to require advanced spatial description techniques. Therefore, if the concept of calculus were to be copied by architecture, it would suggest the possibility of describing architectural space from a different angle, which has not yet been described, and which still leaves a lot of room for exploration. Mathematical space has developed from the basic 3-dimensional space to distance space defined by trigonometric inequalities, to N-dimensional space, to infinite dimensional space (Hilbert space), and then to the height of extremely abstract topological space that encompasses all of these spaces. These are now at the extreme north of abstraction, which defies simple, intuitive grasping. For example, it would be extremely difficult for many people to instantaneously envision n-dimensional space in a conceivable form. However, this is why these mathematical higher dimensional concepts have the potential to describe the sign of an "empirical space" (Poincaré) that cannot be verbalized, which is created by the aspect of architectural space. For example, Guidion et al. viewed the architectural space of modern architecture as a four-dimensional space with a time dimension added to the three dimensions. Similarly, Malevich and Lissitzky, who were at the center of Russian Constructivism, also clearly left a study that envisioned a four-dimensional space. However, if we take this to a higher level and redefine architectural space as an N-dimensional space, we may be able to see a new cross-section of architectural aspects. In any case, as we have seen, looking at the history of calculus from its prehistory to its posthistory, the geometrical figure of the circle as a static world model has transitioned from an ellipse to a cycloid, and then to a curved higher-dimensional space itself, while increasing in dimension and encompassing the movement itself. The trajectory of the project becomes visible. Therefore, the transition over curves has always been in close proximity to architecture as an object frozen in motion. 10 Architecture and Cycloids As a matter of fact, the cycloid curve has been suggested to be related to architecture since its beginnings. As already mentioned, this curve has two characteristics, the fastest descent and the isochronous curve, which means that it is defined by time, motion, and gravity. This is the very essence of what makes architecture, as a physical object and as the cyclic world that humans perceive, architecture. This is why, for example, Galileo himself, who discovered this curve, predicted from the beginning that it would be ideal for the form of an arch bridge and tried to incorporate it into reality, but at the time, he could not yet successfully elucidate its principles. Compared to arches with regular circles, cycloids form flat arches that spread out horizontally and can be approximated as multi-centered circles with many centers of arcs. Therefore, arch bridges that can be regarded as pseudo-cycloidal curves have existed for a long time. For example, the Santa Trinita Bridge in Florence is a six-core circular arch. That is, it is constructed as a pseudo-smooth arch by connecting six arcs. On the other hand, since the cycloid curve can be approximated to a five-core circular arch without limit, the proportions of the Santa Trinita Bridge can be almost superimposed on the cycloid curveNote 17). In addition, "teruori" or "mukuri" roofs are often seen on traditional Japanese and Asian temples and shrines, which are closely related to rainwater treatment and rain control in high rainfall areas. The name "nagare-zukuri" refers to the shape of the roof, which literally means "flowing water," and it is clear that the shape of the roof reflects the flow and behavior of water due to gravity. For example, the shingled roof of the Kondo Hall of Horyuji Temple can be approximated almost as a cycloid curve (Fig. 16). Considering that a cycloid is the fastest descending curve, the builders of the time intuitively saw that this form would lead rainwater from the roof surface to the bottom most quickly. In fact, this kondo has an even more sloped roof than the cycloid. This is a more realistic and optimized version, considering the viscosity and friction of the actual water.

However, above all, the architecture that immediately comes to mind when talking about cycloid curves is Louis Kahn's (1901-1974)Kimbell Art Museum (1972) (Fig. 17).A six-volt museum that, after many trials and errors, finally achieved a precise cycloidal The roof shape was realized as a curved roof. Kahn's use of cycloids here vividly integrates different architectural dimensions: structure and equipment, light and landscape. The cycloidal design keeps the height of the building lower than that of the regular circular vault, creating a spatial effect that softly diffuses indirect light from the central slit to the ceiling surface. Here, a concrete roof with a span of 30 meters by post-tensioning is supported by columns at each of the four corners, and it is said that this curve was chosen because of the structural requirement to uniform the vertical stresses. However, the cycloid here was chosen as a spatial dialectic of "light and power," which Kahn continued to think about throughout his life. It was the form chosen to represent the rationale for channeling power along a curved surface, while at the same time allowing the natural light pouring down to flow smoothly and slowly along the ceiling surface. It was, so to speak, the slowest descending surface of light, stretching the cycloid's physical characteristics of the fastest descending line inverted. It could be said to be a metaphor for gravity and movement, representing a delay, and by sending a sign of space throughout as slowly and as long as possible, the light itself descends and pours down with infinite delay. The cycloid created the unique, grainy atmosphere of this architectural space.

In this sense, Kahn's architecture was a building delicately connected to the calculus of architecture. Beyond that, it was also an architecture that repeatedly evoked the philosophical question of what space is, a question that has been going on from far off in the distance. This essay on the asymptotics of calculus and architecture ends with Kahn's Kimbell Art Museum. However, what has repeatedly emerged throughout this history is the inescapable and important question of "how to posit space in architecture. In other words, if one wanted to think about calculus in the context of architecture, one would have no choice but to arrive at a theory of space. However, the subject of spatial theory in general is so huge and difficult that it is beyond the scope of the author's ability to deal with it. However, when we translate it into architecture, we can see how it intersects with the definition of space in philosophical thought (Descartes, Kant, Bergson, etc.) and in natural science (Newton, Leibniz, Gauss, Riemann, etc.) and at what horizon we can read something new. This is an issue that should be considered now. A new metaphysical theory of architectural space for a new era should be desired, and this paper is a modest attempt toward that end.
Yasuhiro Minami / Architect, Professor at Kokushikan University Born in Hyogo prefecture in 1967. Graduated from the Department of Architecture, Faculty of Engineering, Kyoto University in 1991. Completed the master's program at the University of Tokyo Graduate School in 1993. Enrolled the doctoral program at the same graduate school in 1997. In the same year, Founded the first-class architect office Atelier Implexe. In 2007, associate professor at the Faculty of Science and Engineering, Kokushikan University. In 2012, professor at the university. In 2015, visiting professor at Mimar Sinan Fine Arts University in Istanbul. Works include "PARK HOUSE", "spin-off" and "Atelier Cantere". Books include "How Housing is Possible?" (University of Tokyo Press), "Traverse" (Kajima Institute Publishing), "Recuction of Architecture" (Seidosha), and "Architectural Design Concept" (Shokokusha).
References 1) Masahito Takase: The Birth of Calculus, SB Creative, 2015 2) Yasuo Matsushita: Secrets of Curves, Kodansha, 2016. 3) Hidetaka Terasaka: The World of Non-Euclidean Geometry, Kodansha, 2014 4) Yasunobu Kouchi: Cycloids and Catenary, University Education Press, 2005 5) Hiraku Toyama: Infinity and Continuity, Iwanami Shoten, 1952 6) Newton Supplement: Differentiation and Integration, Newton Press, 2020 7) René Descartes, translated by Hara Kyokichi: Geometry, Chikuma Shobo, 2013 8) Rene Descartes, translated by Juichi Katsura: Principles of Philosophy, Iwanami Shoten, 1964 9) Leibniz, Torataro Shimomura et al. editors, translated by Nobuo Miura: Leibniz Works 2 - Mathematical Theory and Mathematics, Kosakusha, 1997 10) Leibniz, translated by Masaru Yoneyama: New Theory of Human Intellect, Misuzu Shobo, 1987 11) Hide Ishiguro: Philosophy of Leibniz, Iwanami Shoten, 1984 12) World Famous Books 30: Leibniz, Spinoza, edited by Torataro Shimomura, translated by Tomio Shimizu et al: Monadology, Chuokoronsha, 1980 13) Nicolaus Cusanus, translated by Keizo Yamada: On Learned Ignorance, Heibonsha, 1994 14) Gilles Deleuze, translated by Osamu Zaitsu: Difference and Repetition, Kawade Shobo Shinsha, 1992 15) Gilles Deleuze, translated by Kunikazu Uno: Folds, Kawade Shobo Shinsha, 1998 16) Bergson, Hirai Hiroyuki, Translation: Time and Freedom, Hakusuisha, 1990 17) Bergson, translated by Naoki Sugiyama: Matter and Memory, Kodansha, 2019 18) Bergson, translated by Takamichi Magata: Creative Evolution, Iwanami Shoten, 1979 18) Aristotle: Metaphysics, translated by Tsutomu Iwasaki: Kodansha, 1994 19) Edmund Husserl, Jacques Derrida, translated by Setsuo Tajima et al: The Origin of Geometry, Seidosha, 1992 20) Hideki Yukawa: The World in a Book, Iwanami Shoten, 1963 21) Kunio Ota: Ethno Architecture, Kajima Press, 2010 22) Tetsuo Ito: Forest and Ellipse, Inoue Shoin, 1992 23) Morita Keiichi: Outline of Western Architectural History, Shokokusha, 1962 24) Architectural Institute of Japan (ed.): Illustrated History of Western Architecture, Shokokusha, 1953 25) Christian Norberg-Schulz, translated by Kunio Kato: Illustrated History of World Architecture 11 Baroque Architecture, published by Hon no Tomosha, 2001 26) Louis Kahn, translated by Tadanao Maeda: Louis Kahn Architectural Essays, Kajima Publishing House, 1992 27) Architectural Institute of Japan, Architectural Magazine, No. 93, 95, 96, 1894 28) Le Corbusier, translated by Kiyoshi Higuchi: Urbanisme, Kajima Press, 1967 Note Note 1) Reference 27) Note 2) See reference 21),pp.81-158, chapter "Why Architecture Became Square". Note 3) Reference 20),pp.177-178 Note 4) Reference 28) Note 5) Reference 7), pp. 029 Note 6) Reference 8), pp. 128 Note 7) Reference 22), pp. 154 Note 8) Reference 9), pp. 68 Note 9) Reference 19), pp. 111 Note 10) Reference 5), pp. 51 Note 11) Reference 25), pp. 124 Note 12) Reference 13), pp. 121 Note 13) Reference 12), pp. 435-460 Note 14) Reference 14), pp. 269 Note 15) Reference 10), pp. 210 Note 16) Ibid. note 8), pp. 28 Note 17) Reference 4), pp. 42-45 Fig.1 Ptolemy's celestial model of the universe (1524). Source: Wikipedia Fig.2 Ruins of the amphitheater at Miletus, Ionia, Turkey. Photo: Yasuko Minami Fig.3 Pantheon (Rome, 118-128). Photo by the author Fig.4 Colosseum (Rome, 72-80). Photo by the author Fig.5 Copernicus' geocentric model of the universe (1543). Source: same fig.1 Fig.6 Elliptical motion and area velocity of celestial bodies according to Kepler's laws. Source: Encyclopedia of Japan (Shogakukan, 1984~1994) Fig.7 Discussion of circular motion by Descartes. Source: "Principles of Philosophy", Reference 8) Fig.8 Piazza del Campidoglio (Michelangelo, Rome, 1536-47). Photo by the author Fig.9 Church of Sant'Andrea (Vignola, Rome, 1553). Source: Asian profile Fig.10 San Carlo alle Quattro Fontane, exterior and floor plan (Borromini, Rome, 1638-46). Source: same fig. 1. Fig.11: Sant'Andrea al Quirinale, exterior and plan (Bernini, Rome, 1658-1670). Source: ibid. fig.1 Fig.12 St. Peter's Square (Bernini, Rome, 1656). Photo by the author Fig.13 Court library (Erlach, Vienna, 1723). Source: Wien Tourismus. Fig.14 Cycloid curve. Source: monozukuri.sqcd-aid.com Fig.15 St. Paul's Cathedral, exterior and plan (Christopher Wren, London, 1710). Source: same fig.1 Fig.16 Kondo and five-storied pagoda of Horyuji Temple (Nara, 7th century). Source: ibid. fig.1 Fig.17 Kimbell Art Museum (Louis Kahn, Fort Worth, 1972). Source: ibid. fig.1
